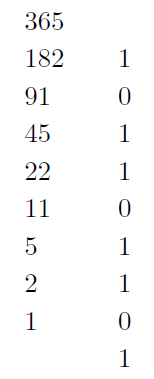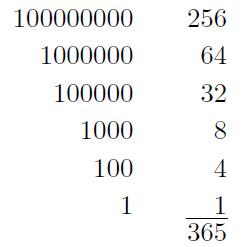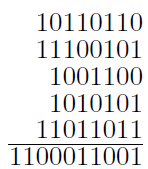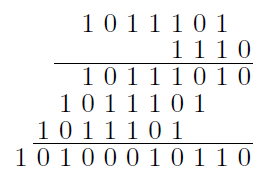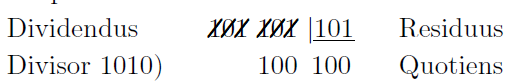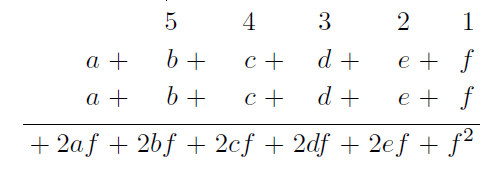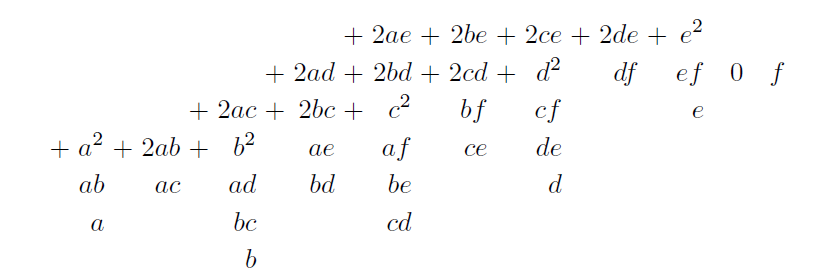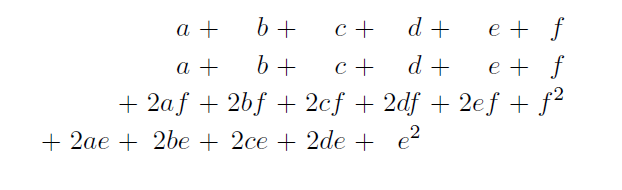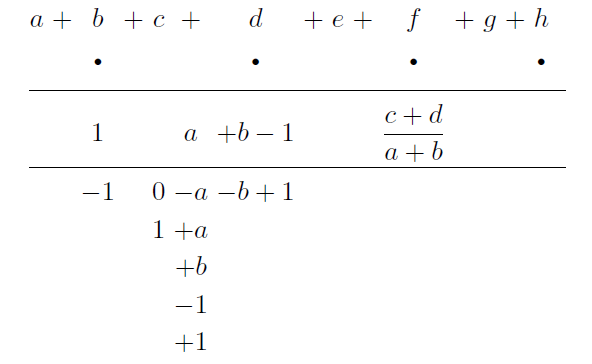Transcription of De Progressione Dyadica (1967)
(Transcription kindly provided by the Leibniz-Archiv)
De Progressione Dyadica.
Pars I.
Numeratio
Adscripta progressio facile continuari potest, eundo a dextra sinistrorsum, et superstantis numeri unitati subscribere 0. Donec occurrat in superstante etiam 0. cui subscribitur 1. nec ultra pergi opus, nam reliqui characteres manent ut in superstante, ita ex 1010111 87. Idem est ac si diceres: 1011000 esse 2^6[64]+﹡+2^4[+16]+2^3[8]+﹡﹡﹡ fit 1011000 88
Nam 1 in quarto loco seu 1000, significat cubum fundamenti progressionis, uti enim in communi progressione significat cubum a denario seu mille. Ita in nostra cubum a binario, nempe octo. Similiter 1 in quinto loco significat quadratoquadratum seu 16, et in sexto significat surdesolidum seu 32, et in septimo deinque quadratocubum seu 64.
Notandum si in progressione descendas perpendiculariter a charactere numeri superioris ad characteres directe subjectos numerorum inferiorum, semper unitates redire per saltos, et in ultimo loco redicere unitatem post unum zero. At in secundo loco seu quadraticam radire post tria, in tertio loco cubicam post septem zero interjecta, in quarto loco seu quadratoquadraticam post quindecim.
Hinc jam offerre se videtur modus commodus transformandi expressionem dati numeri decadicam in dyadicam, sit numerus 36[5] ejus continue sumatur dimidium et dimidium dimidii, residuo semper e regione medietates scripto, et characteres ordine scripti ita ut imus sit sinisterrimus, et ita porro, dabunt expressionem dyadicam quaesitam.
Eadem methodus servari potest pro quacunque progressione in aliam commutanda. Itaque 365 erit 101101101, nempe
Simili arte dyadicus convertetur in decadicum, vel addendo in unum omnes binarii potestates decadice expressas, ut hoc loco 256. 64. etc. vel etiam dyadicum datum dividendo per denarium decadice expressum, residuis ordine collocatis, eodem quo quo dixi modo:
Additio Numerorum hac methodo tam facilis est ut non citius possint dictari, quam addi ita ut non scribi necesse sit numeros, sed statim scribi possint summas Exempli Causa dictatur mihi
primum 10110
postea 11011
scribo statim 1000001
sed si columnes plures addendae ut
numera unitates columnae, si numerus par scribatur sub ea unitas, et dimidius numerus unitatum ascribatur columnae sequenti sive punctis sive numeris communibus itaque ad addendum in hac progressione opus est tantum posse numerare unitates; cum in aliis opus sit saltem addere posse numeros simplices, verbi gratia 8 et 5 facit 13. qui hoc non novit commode addere in decadica progressione non potest.
Eadem methodo facillime procedit subtractio, imo et mixtio additionis et substractionis tantum enim colligendae unitates. Quando autem miscetur additioni subtractio, cuilibet detrahendae respondens numeretur addenda: nam hae se invicem destruunt. Verbi gratia:
In columna A. incipi ab L. ubi 1 est cum signo + Ergo punctetur simul hoc 1 cum alio 1. quod est in P. cum signo — similiter in M est +1. punctetur cum -1 in S. Denique in N est +1. punctetur una cum -1. in W. erunt omnia -1. punctata et restabunt +1 non punctata quae numerentur ac si sola adessent, et sequenti columnae ascribantur cum suo signo, hoco loco +, alias — si plura fuissent -1. Est et hoc notandum pro numero subtrahendo posse poni ejus supplementum ad 100000 etc., et ita non opus esse subtractione, sed tantum additione, ea methodo qua id fieri etiam in decadica alibi demonstravi ut subtrahendus est numerus 110101, ponatur
statim autem scribi potest supplementatis hoc modo, si in primo a dextris charactere subscribatur idem, in reliquis contrarius, mutando scilicet 0 in 1 et 1 in 0. Tandem sub nem notandum, sequenti columnae, ad quam nullus ex subtrahendo character pertingit subtrahendum unitatem, si subtractionem per solam supplementatam additionem peragere volumus.
Transeo ad Multiplicationem. Ubi rursus patet nihil facilius fingi posse. Nam nulla opus est Tabula Pythagorica: Et hoc sola est multiplicatio nullam aliam multiplicationem jam notam praesuppones. Tantum enim scribantur numerus aut ejus loco 0.
Hujusmodi calculus fieri posset per machinam. Hoc modo sane facillimo et sine sumtu.
Si pyxis perforata, ita ut foramina aperiri et claudi possint, aperta in locis respondentibus ipsis 1. clausa manens in locis respondentibus ipsis 0. per loca aperta deponat cubulos vel orbiculos in crenas, per alios nihil, et ita promota et de columnis in columnas transportata, ut multiplicatio postulat, crenae repraesentent columnas nec possit orbiculus ex una crena in aliam ire, nisi postea mota machinulta, ubi globuli effluent omnes in sequentem crenam, demto semper uno qui in foramen manet; si quidem per portam transire vult solus nam res ita institui potest, ut duo semper simul effluant necessario, alioqui non effluent;
Divisio in hoc calculo fit tum sine tabula Pythagorica, tam etiam sine tentatione. Videamus quomodo compendiosissime.
te quasi adesset 1 loco 0. verum in sequenti 1. debet fieri 0 ex ipso, quid si vero non sequatur 1. sed 0. tunc omnia 0 quae sequuntur, mutantur in 1, et primum 1. quod ea excipit (eundo a dextro versus sinistrum) mutatur in 0. prorsus ut in decadica, nisi quod ibi mutantur 0 in 9.
Hactenus Algorithmum habuimus progressionis hujus. Venio ad ejus Algebram, quam alia plane quam vulgo ratione intelligo nam incognitas assumam, non pro quantitatibus incognitis sed pro characteribus numeros quaesitos Dyadice expressos designantibus. Quod hactenus nemo fecit. Mirifice autem hoc artificio contrahuntur omnia. Nam incognitus character adeo prope cognitus est, ut hoc unum tantum supersit de eo quaerendum, utrum sit 1 an 0. Deinde quod est admirabile incognitorum quadrata aut cubi aut aliae quacunque potentiae nihil turbant, ut in Algebra communi, nam quia character incognitus significat, 1. aut 0., ideo quadratum ejus idem significat quod ipsemet, nam ipsius 1 quadratus cubus etc. est 1 quemadmodum potestas ipsius 0. est 0. Itaque si unquam hic certe omnia ad simplicissimas expressiones reducuntur, neque enim nisi, unitate et Zero indigemus. Adde et nihil posse fingi universalius. Ostendam enim et fractas et irrationales, imo et transcendentes quantitates, ut logarithmos et angulos seu arcus hoc modo quantum possibile est determinari posse.
Sit ergo numerus quicunque dyadicus integer, finitus (vel pro fractis et irrationalibus et transcendentibus finitis) infinitus
Ejus quadratum quaenam conjungatur facile aestimari potest ex dimensionibus nempe a^2 vel a est 12 dimensi. ab est 11. dimensionum sed fit 12, quia duplicatum fuiit. ac est 10 dimensionum sed fit 11. ad est 10 dimensionum, item b. item bc. et ita de caeteris.
Ubi notandum prout litera aliqua significat 1. vel 0. oriri aliam atque aliam provenientis numeri expressionem dyadicam. Haec tamen interim afferri possunt pro certis characterem penultimi producti quadrati dyadici semper fore Zero. Item qualis est penultimus lateris, tales est antepenultimus quadrati.
Si duo postremi lateris sunt ambo 1. antepenultimus quadrati erit 0. aliqui erit 1. Imo melius, si f est 1. semper antepenultimus quadrati est 0. nam si e est 0. patet, si e est 1. tunc fieret 2. Ergo 0. Si e est 0 semper antepenultimus est 0. si e est 1 et f est 0. tunc semper est 1. Ergo ex his duobus ultimo et penultimo lateris determinati sunt tres ultimi quadrati.
Si in radice tres ultimi sunt 1. erunt in quadrato tres ante ultimum, in 0. et generaliter si sit radix quotcunque unitatum, erit quadratum ejus compositum ex terminis quorum primus et ultimus 1. intermedii vero 0.
Pars II.
Absolvimus Scheda praecedente Algorithmum, seu quatuor quas vocant operationum species in dyadica progressione exhibitas: Unde perreximus ad Potestates puras earumque latera; et incepimus a simplicissimo omnium quadrato. Ubi schema tale dedimus:
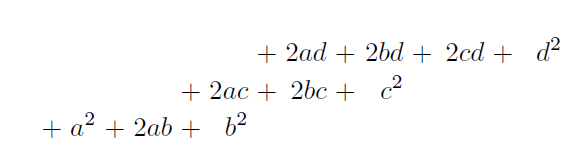
Unde ob dyadicam progressionem transferendo in sequentem columnam quae binarium excedunt et pro characterum potestatibus ponendo ipsos simpliciter fiet.
Ut jam relationem inter characteres lateris et potestatis investigemus incipiemus quidem ab ultimis characteribus ad determinados characteres potestatis ex characteribus lateris; seu ad genesin: sed contrarium faciemus, et a primis characteribus conferendis incipiemus ad determinandos characteres lateris ex characteribus potestatis seu ad analysin. Ante omnia illud certum est: ultimum characterem lateris et quadrati esse eundem.
Penultimus character quadrati semper est 0. Si penultimus lateris character est 0, antepenultimus quadrati est 0. Nam si e est 0 etiam ef+e est 0. Si ultimus lateris character est 1. tunc antepenultimus quadrati erit 0. Nam si f est 1 tunc e vel erit 0 vel 1. Si f existente 1 e est 0. Tunc character de quo agitur est 0 per praecedentem. Si f existente 1. ipse e est etiam 1 tunc ef+e est 2. Ergo character est 0. nempe unitate ob 2 translata in columnam sinisteriorem.
Si ultimus lateris character est 0. et penultimus 1. (qui casus solus superest) erit quadrati character antepenultimus 1. nam si f est 0 et e est 1 erit ef+e aequ. 1.
Si ultimus lateris character est 0. tunc etiam penantepenultimus quadrati est 0. Nam si f est 0. tunc df destruitur in hac columna penantepenultima, nec quicquam accipitur a praecedente, quae f existente 0. tantem habet e seu 1 vel 0. Si d et f sunt 1. et e est 0. tunc solum penantepenultimus quadrati est 1.
Columna penantenultima tum demum 1. transmittit in sequentem cum d. e. f. sunt et tunc ipsa fit 0.
Similiter columna antepenantepenultima tum demum transmittit aliquid in sequentem cum ipsa est 0. nisi hoc unico casu cum f. c. e. existunt et c est 0. id est cum existit ultimus quadrati et penultimus, et antepenultimus et penantepenultimus sunt 0. Nam cum transmittit aliquid in sequentem non consistit nisi ex quatuor vel duobus terminis seu unitatibus vel uno. Numquam ex tribus quod sic ostendo: a pracedente columna non accipit nisi unitatem ponatur jam non accipere, tunc in columna hac erit 0. Nam si non accipit, tunc per praecedentem vel d vel e , vel f est 0. si d. restabit cf+d . id est 2 ergo
transmittitur 1. in sequentem et restat 0. Denique si f est 0. restat de+d id est vel 1 vel 2. nunquam 3. Si accipit unitatem ex praecedente, tunc existunt d. e. f. Ergo columna haec facit 4. nisi c . existat 0 tunc facit 3.
Analysis seu inquisitio lateris ex dato quadrato:
Pono a primum characterem lateris non esse 0. sed 1. alioqui non ab ipso incipiemus sed a b. Eandem ob causam pono primum characterem potestatis esse 1. nam non potest esse major, neque minor alias foret 0.
Fiat primum punctatio communi more tunc si abest K necessario b. est 0. sed cuncta calculo exprimamus analytice. a aequ. 1. b aequ. K + L — 1. id est si K absit tunc b est si L absit tunc b est 1. si KL absit tunc b est 10, id est b est 0. nam 1. pertinet ad a .
Sed jam video tales calculos esse inutiles quia nescimus semper quid acceperit columnaa dexteriore. Si vero incipimus a dextris comparando f et X, tunc non servit calculus noster nisi illis casisbus ubi quaeritur an exacte sit quadratus, is de quo agitur, numerus, quanquam hac methodo comparando cum exacte quadrato, videamur posse consequi quod quaeritur quam minimum auferendo, ut fiat datus numerus patiens legum. Et haec quidem analysis certa est genesi respondens et pro omnibus potestatibus puris et affectis universalis.
Esse tamen videtur et alia methodus investigandi radicem, per extractionem generalem. Sit ergo
Omnis quantitas analytica ad quantitatem revocari potest hujus formae, a+by+cy^2 etc. aequ. l+my+ny^2 etc. Ita nulla opus distinctione inter + et — merae enim sunt affirmativae etsi forsan aliqua desinit. Inveniatur seriei periodus et exponatur certo characteris genere, ut in locis curvarum, ita facile investigari poterit quae sit periodus quadrati cubi, et quid prodeat. Si formula infinita periodica in finitam multiplicetur aequandae sunt tandem duae series ab utroque latere; si quidem id possibile est. Tentemus rem in aliis problematis ubi scimus aliquam esse aequationem quam hoc modo inveniemus.
Sed video hoc fieri nimis difficile; si rem generaliter seu literis persequi velimus.
Itaque priori viae analyticae supra dictae insistentem. Numero tamen quovis in specie oblato rem consequi non difficile est.
Sed omissis tantis per potestatibus explicemus prius quantitates fractas per minutias dyadicas.
Ut autem generaliter discatur relatio inter numerum, et ejus fractionem dyadice expressam sumantur series generales periodicae a minoribus periodis ascendendo ad majores, et ejusmodi series multiplicetur per numerum finitum quantum satis generalem, et determinetur quibus modis fieri possit, ut in producto omnia destruantur, seu fiant 0, exceptis paucis terminis primis. Forte licebit melius sic agere. Sume seriem infinitam generalem nulla mentione periodorum, hanc multiplica per numerum finitum; in producto omnia destruenda sunt praeter primam unitatem. Et ita haberi potest modus exhibendi fractionem simplicem, seu cujus numerator est unitas. Derivatae, quarum numerator est numerus horum per illum numerum multiplicatione habentur. Quanquam et hoc modo haberi et generaliter determinari possit, quae dati Numeri periodis in infinitum reccurrentibus expressi sit summa. Ita ut vicissim ex data expressione periodica habeatur summa, seu numerus, ut paulo ante ex dato numero expressionem periodicam dyadicam comparatione ducendam diximus.
Habita periodo ex dato numero, habebitur etiam modus exprimendi certa regula seriem characterum magnitudinem circuli exprimentium seu \frac{1}{1}-\frac{1}{3}+\frac{1}{5}-\frac{1}{7}+\frac{1}{9} etc.
Sed illa potissima inquisitio est, et totius analyseos caput, utrum quaelibet quantitas sit analytica.
Sumatur scilicet quaecunque series characterum, regulam habens, secundum quam continuatur, quaeritur si hujus seriei scribantur ordine potentiae quotcunque, numero finitae singulaeque ductae intelligantur in numeros finitos, (x^0. est etiam potentia, nempe cujus exponens est 1) eaque producta quibuscunque signis invicem addantur, quaeritur an semper fieri possit, ut omnia simul se destruant. An vero fingi possit series quae nullo modo possit destrui per has methodos. Et jam video hujusmodi series analytice non exprimendas fingi posse, pone enim seriem aliquam ita fieri: sumatur numerus, aliquis constituens primam seriei periodum secunda periodus sit aliqua potentia radixque pura vel affecta prioris, tertia periodus, rursus alia altior, et ita porro in infinitum novis perpetuo arbitrariis assumtis literis. Non videtur semper possibile esse postea tales assumere exaltationes et involutiones affectes finitas, quibus tola illa moles destruatur nam literas paucas finitas arbitrarias quae assumi possunt, impossibile est satisfacere infinitis illis semper variantibus literis, quae utcunque a se invicem diversae assumi possunt. Demonstratum est ergo dari quantitates transcendentes seu quae aequatione certi gradus exprimi non possunt. Sed an talis sit area circuli speciatim examinandum. Imo jam video ne hoc quidem demonstratum esse quod dantur quantitates non-analyticae nam si quantitas est determinata, non utique istae literae assumendae ad potestates affectas pro sequentibus periodis possunt esse arbitrariae, sed ex determinatis etiam finitis conditionibus oriuntur.
Necesse est dari periodum aliquam postquam nulla sit nova litera vel quantitas assumta, sed quoniam fieri potest, ut in sequenti periodo in valde magnam seriem extendantur, et in tertia adhuc in majore in infinitum: dubito an finitae exaltationes his destruendis sufficere possint.