See a translation for the manuscript
Overview of Periodus numerorum (1705?)
Periodus Numerorum is a manuscript written by Overbeck for Leibniz in around 1705 and represents a collection of results obtained by Leibniz on the topic of dyadics. The content of the manuscript strongly suggests that it was dictated word by word by Leibniz, as that level of knowledge of the binary system it includes was available only to him at that time.
The manuscript starts by introducing a new notation to express what had already been defined by Leibniz in other manuscripts as the period of natural numbers:
0_{1024}1_{1024}|0_{512}1_{512}|0_{256}1_{256}|0_{128}1_{128}|0_{64}1_{64}|0_{32}1_{32}|0_{16}1_{16}|0_{8}1_{8}|0_{4}1_{4}|0_{2}1_{2}|0_{1}1_{1}=N
20\ \ \ \ \ \ \ 19\ \ \ \ \ \ \ \ \ \ 18\ \ \ \ \ \ \ \ \ 17\ \ \ \ \ \ \ \ \ 16\ \ \ \ \ \ \ \ 15\ \ \ \ \ \ \ \ 14\ \ \ \ \ \ 13\ \ \ \ \ 12\ \ \ \ 11\ \ \ 10
What Leibniz means with this notation is that any natural positive integer can be written in a dyadic form, keeping in mind that every digit (presented from right to left) will also belong to a period of alternating zeroes and ones, as shown in the tables of De progressione dyadica, or as represented here by the number of repeating zeroes and ones specified by the subscripts. In fact, if we write the progression of every positive integer in the form of a table we obtain the same period expressed by Leibniz in his new notation:
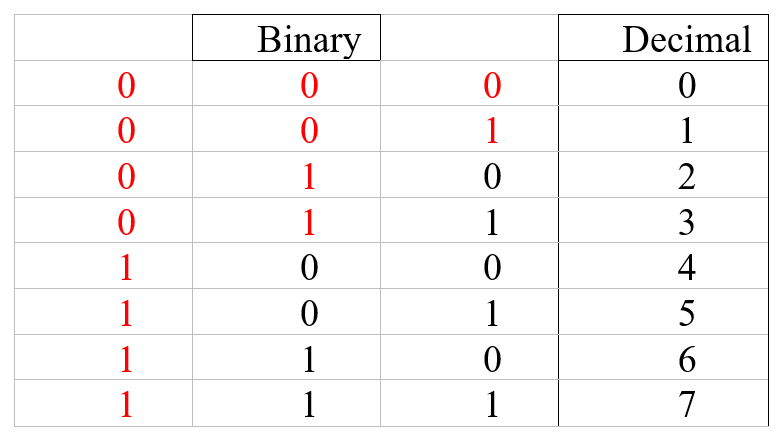
The text then shifts its attention from this new unique way of expressing these numbers to their algebraization, following the development of De progressione dyadica manuscript. This time however, instead of using generic letters for the algebraization, Leibniz choose to implement numbers having the function of algebraic letters, a method he had already used in another manuscript published by Zacher (the Summum calculi analytici fastigium), to better convey the fact that there can be as many digits in these numbers as we want, as they are positive integers of an infinite set.
Once these numbers, also called fictive numbers in the mathematical tradition, are assigned to every binary digit, Leibniz shows the relationship between two algorithms for the expansion of a square, the first one valid in any numeral system and the second one valid only for the binary numeral system, following again the Summum calculi analytici fastigium (Zacher 1973, 220):

The first table shows the expansion of a square in the form (a+b…)^2, while the second describes another expansion valid only for numbers expressed in the binary system. This result is relatively independent from the rest of the manuscript, because it can be obtained ignoring the new notation for the periods introduced by Leibniz, as in fact he does in De progressione dyadica. For a more detailed explanation of the relationship between these two algorithms see Brancato (2021).
Shifting the attention once again to the new way of expressing the period of positive integers presented at the beginning, the manuscript then introduces some laws of calculation valid only in the binary numeral system. In this part of the manuscript Leibniz tries to apply his own rules to describe multiplications and additions between fictive numbers representing periods:

The main idea is that if belonging to a particular column means that a digit has a probability of being 0 or 1 following a certain pattern, investigating the relationship of addition and multiplication between digits belonging to different columns is a legitimate way to determine the new pattern followed by the digit that will be obtained as a result of this combination. These explorations lead Leibniz to a general rule connecting fictive numbers and periods: 1m\times1n=0_{2^m}\left(0_n1_n\right)_{2^{m-n-1}}, where m and n represent any possible second part of a fictive number.