See a transcription for the manuscript
Translation of De curvis similibus et similiter positis et parallelis (1685) (Partial translation) [FRN]
Je me suis longtemps demandé si deux courbes inégales (en dehors des cercles) pouvaient être exactement semblables, par ex. deux Ellipses, deux paraboles, etc. J’avais en effet noté qu’un cercle pouvait être équidistant partout à un autre cercle, alors qu’une courbe équidistante à une Ellipse ou à une autre courbe n’était pas une Ellipse, ou une courbe du même nom qu’elle. Et il me semblait que deux courbes semblables et semblablement placées devaient être parallèles, mais à présent j’ai compris que ce n’était pas nécessaire (si le parallélisme est pris comme l’équidistance, ou si le parallélisme est pris à partir de ces angles que font des droites parallèles menées de même façon, à partir de points posés de même façon, aux deux courbes, ou bien des angles que font la même droite menée à partir d’un centre commun). Et j’ai vu que, pour n’importe quelle courbe, on pouvait en exhiber une autre semblable et semblablement placée, si l’on procédait à sa génération par un principe semblable ou indiscernable point par point (singulatim)
Par exemple, si l’on décrit ABD, un demi-cercle de centre C et diamètre AD et que l’on prolonge l’une quelconque de ses ordonnées, comme EB, dans un rapport donné jusqu’en F, A F D seront sur une semi-ellipse. Et semblablement si l’on décrit un autre demi-cercle GLH de même centre C et de diamètre GH, dont n’importe quelle ordonnée ML est prolongée en N avec le même rapport que (j’ai dit) ci-dessus, il viendra la semi-ellipse GNH semblable à la précédente et semblablement placée, toutes les choses en effet sont point par point indiscernables dans les deux cas.
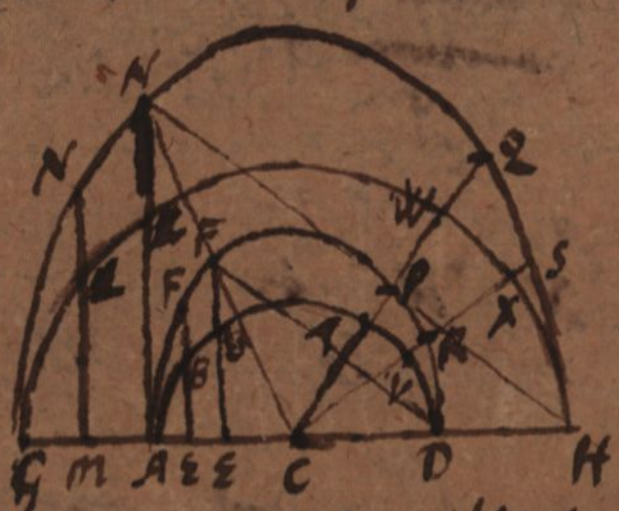
Ainsi, deux circonférences ou Ellipses seront semblables entre elles, comme les axes, mais les aires comme les carrés des axes.
Deux droites menées du centre CPQ, et CRS, rencontrant les deux ellipses FF et NN, la première aux points P et R, la seconde aux points Q et S, découperont des secteurs et aires semblables et semblablement posées, et le secteur PCRP sera au secteur QCSQ comme les aires (l’aire ? area) des ellipses c’est-à-dire comme le carré de AD au carré de GH; c’est-à-dire comme le secteur TCVT correspondant au secteur du cercle générateur le plus petit au secteur correspondant WCXW du cercle générateur le plus grand. Et l’arc Elliptique PR sera à l’arc Elliptique QS, comme l’ arc circulaire PR TV ( ou AV)à l’arc circulaire WX, soit comme AD à GH.
Plus généralement n’importe quelle droite menée à partir du centre rencontre les deux Ellipses avec les mêmes angles, c’est-à-dire que les deux Ellipses sont parallèles en les points P et Q, ou ont même inclinaison, c’est en effet en ce sens que j’entends le parallélisme.
Et ceci aussi certainement si des droites sont menées à partie d’un point qui remplit la même fonction dans les deux cas, comme le centre commun, n’est-ce pas. Mais si l’on prend deux points différents dans deux Ellipses différentes, et remplissant la même fonction, comme les sommets vertices) ( pour le moment je ne dis rien des foyers) et que l’on mène à partir d’eux deux droites parallèles, comme DF, HN, la même chose sera prouvée à partir de ces droites parallèles, que dans le cas des mêmes menées du centre de sorte que les segments DFPD, HNQH seront aussi entre eux comme le carré de leurs axes et leurs arcs comme les axes et ils rencontrent les courbes sous les mêmes angles et les droites parallèles sont entre elles comme la courbe parallèle à la courbe présente (ibi) et ont certainement en N la même inclinaison qu’en F, en effet la droite CFN aussi rencontre les deux en partant du centre.Il en sera de même si ce ne sont pas , comme jusqu’ici, des droites, mais d’autres courbes semblables et placées semblablement qui sont menées, elles coupent aussi des parties proportionnelles de circonférence et d’aires et rencontrent les deux sous les mêmes angles.
[…]
De plus, le nœud s’est ainsi résolu pour moi, et la vraie nature de la similitude et du parallélisme qui me tourmentait depuis longtemps est arrivée à ma connaissance ; puisque je comprends assez bien a priori qu’une figure quelle qu’elle soit puisse être contractée ou expansée dans une autre plus petite ou plus grande similaire en toute chose et semblablement posée, et que néanmoins , en menant une ligne parallèle à une ligne au sens où une droite perpendiculaire à une droite est aussi perpendiculaire à une autre [droite] (dans ce cas elles sont équidistantes) j’obtiendrais des courbes tout à fait dissemblables.