See a transcription for the manuscript
Translation of De curvis similibus et similiter positis et parallelis (1685) (Partial translation) [ENG]
I doubted just now whether two unequal curves (excluding circles) could be exactly similar, e.g two ellipses, two parabolas, etc. Since I noted that a circle can be equidistant everywhere to a circle, but that a curve equidistant to an ellipse or to another curve is not an ellipse, or a curve of the same denomination as the original curve. And it seemed to me that two curves, both similar and posited similarly, had to be with necessity parallel, but just now I notice indeed that it is not necessary (if parallelism is taken to be through equidistance, or if parallelism is assumed to be from equal angles which two curves make with parallel straight lines led out from similarly posited points or to the same straight line led out from a common center). And I saw that, to an arbitrary curve, another one similar and similarly posited can be exhibited if its generation has a similar, or indiscernible, principle.
E.g. if semicircle ABD is described with center C and diameter AD and an arbitrary ordinate EB is produced with a given ratio to [F], AFD is a semi-ellipse. And similarly another semicircle GLH is described with the same center C and with diameter GH and an arbitrary ordinate ML is produced with the same ratio as I had said before to N, then the semi-ellipse GNH is similar and similarly posited to the prior, since everything is indiscernible considering the figures one by one.
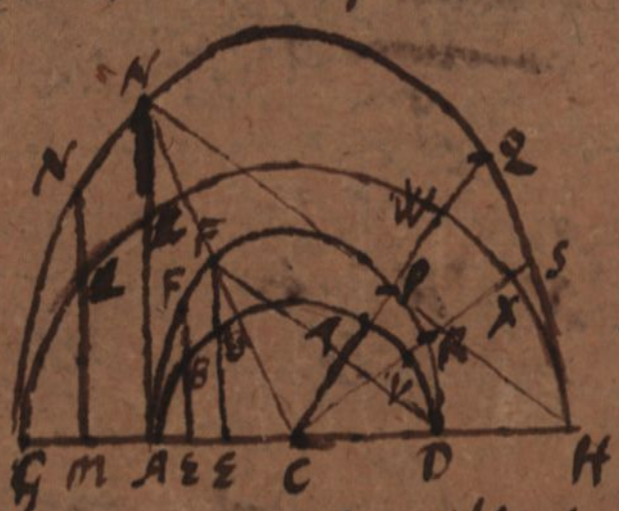
Hence the two similar circumferences or ellipses are among themselves as the axes, and indeed their areas as the square of the axes.
When two straight lines CPQ and CRS are drawn from the center, meeting the two ellipses FF and NN, the first at the points P and R, the second at the points Q and S, they cut sectors and areas that are similar and similarly posited, the sector PCRP will be to the sector QCSQ just as the area of the ellipses or as the square of AD is to the square of GH; or just as the sector TCVT of the corresponding smaller generating circle is to the sector WCXW of the corresponding greater generating circle. And the elliptic arc PR will be to the elliptic arc QS as the circular arc [TV] is to the circular arc WX, or as AD to GH.
More generally, when a straight line is drawn out from the center and meets both ellipses with the same angles, the two ellipses are parallel to each other at points P and Q, or they have the same inclination, since I understand parallelism here in this sense.
And this indeed holds if straight lines are led out from a point which makes the same function to both, namely from a common center. But if two diverse points are taken making the same function with diverse ellipses, such as vertices D and H (as now I will say nothing about the foci), and from these points parallel straight lines are led out, namely DF, HN, the same will be proved from these parallel straight lines, that was in the case of those from the same center, so that segments DFPD, HNQH will also be among themselves as the square of their axes, and their arcs as their axes; and they meet the curves at the same angles, and the parallel straight lines are among themselves as the curve parallel to the other curve, and without doubt they have the same inclination towards N as towards F, for the straight line CFN also meets both from the center. It will be the same even if not (as until here) straight lines, but other curves both similar and similarly posited are drawn, and they will also cut proportional parts of the circumferences and areas, and meet both lines in the same angles.
[…]
Moreover in this way I have solved the knot and I have understood the true nature of similarity and parallelism, which had frustrated me for a long time; since I understand well enough, from the preceding reasoning,that any figure can be contracted or expanded into another bigger or smaller figure which is similar in all respects and similarly posited, and nonetheless when I draw a line parallel to a given line in this sense, namely that a straight line perpendicular to one line is perpendicular to the other line (in which case they are equidistant), I obtain curves clearly dissimilar.