See a transcription for the manuscript
Translation of Duae rectae parallelae sunt (Partial translation) [ENG]
Two straight lines are parallel, which being produced, if necessary, hold themselves in the same way everywhere.
If they are such then, when you are in them, they cannot be discerned from each other.
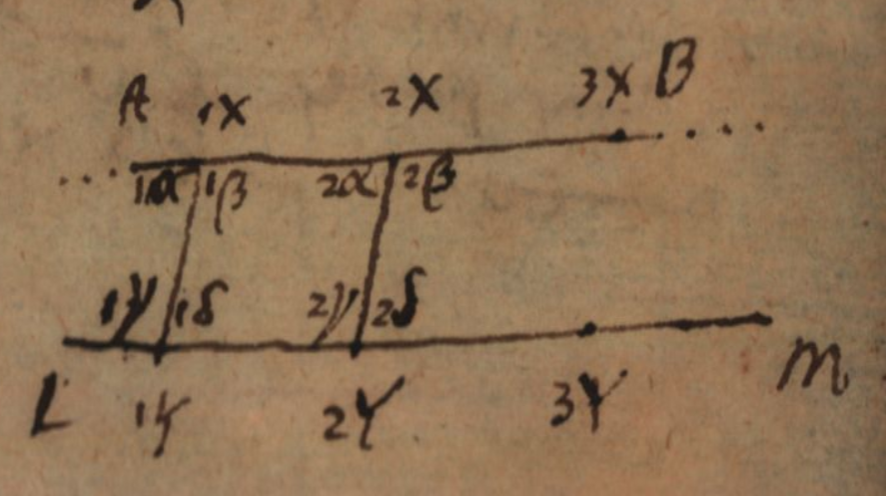
Let AE and LR be straight lines and an observer X be moved along the first, while an observer Y along the second, both moving with an equal uniform motion, and carried so that the situation of 1X1Y and both the situations of the observers among themselves, and the straight lines along which they are moved (since they are indefinite straight lines), cannot be discerned.
Indeed if they are not only always similar, but also equal, the congruent straight lines will be parallel lines. But it is necessary that this relationship is not referred to some fixed point, such as A or L, otherwise the situation of one can be discerned from the other either through access or regress with respect to the fixed point. Therefore, if 1X2X=1Y2Y, we have 1X.1Y.X̅.Ȳ≃2X.2Y.X̅.Ȳ.
[…]
[A long section is crossed out]
Axiom: if similarly determining things are similar, congruent, or coincident; then also their determined things will be such, and vice versa.
If equal straight lines 1X2X, 1Y2Y are cut by two parallels, AB, LM on the same sides, and the beginning is joined to the beginning and the end to the end with two straight lines 1X1Y, and 2X2Y, then all the straight lines will be equal among themselves. For since 1X.1Y.X̅.Ȳ≃2X.2Y.X̅.Ȳ, then also 1X.1Y≃2X.2Y, and thus 1X1Y=2X2Y.

The corresponding angles, which are made to the parallels when the straight lines are joined together, are equal. For if 1X1Y made a different angle to X̅ than 2X2Y, then (because of the axiom) 1X.1Y (these two points determine the straight line 1X1Y) would hold itself to X̅ differently from 2X.2Y, which is against the above theorem, where 1X.1Y.X̅≃2X.2Y.X̅.
The straight lines through 1X, 1Y and through 2X, 2Y are parallel, for they hold themselves in the same way among themselves as the straight lines through 1X, 2X, and through 1Y, 2Y; or, a quadrilateral having equal opposite sides, has parallel sides, and it is a parallelogram.
Parallels are in the same plane. For, in the previous configuration, the plane 1Y1X.X̅ is the same as the plane 2Y2X.X̅, otherwise the prior situation could be distinguished from the posterior. Therefore, 1Y1X and 2Y2X (which are parallel) are in the same plane as straight line X̅. It is shown in the same way that 1Y1X and 2Y2X are in the same plane as straight line Ȳ, therefore the straight lines X̅ and Ȳ are in the same plane.
Another way. If a straight line is given, and a point not on it, a plane common to the straight line and the point will also be given. This point will be in one of two segments of the plane which the straight line makes. Thus, a parallel straight line passing through the point will be in the same plane, since whichever point you like will stand to the straight line, as one point does.
The parallel to a given straight line through a given point is unique. In fact, if one point is given by its situation to the points of a certain straight line, and a segment of a plane is given, then another point is also given among the other points of the straight line situated in the same way among themselves. But, two points being given, a straight line is given.
This is expressed in calculus: let the straight line Ȳ be given, and the point C be given, and let C.Ȳ≃X.Ȳ, then X̅ will be another straight line parallel to the prior through C.