See a transcription for the manuscript
Translation of Duae rectae parallelae sunt (Partial translation) [FRN]
Sont parallèles deux droites, qui étant prolongées, si besoin est, se comportent partout de la même façon.
Si elles sont ainsi où que l’on soit en elles, on ne peut les distinguer.
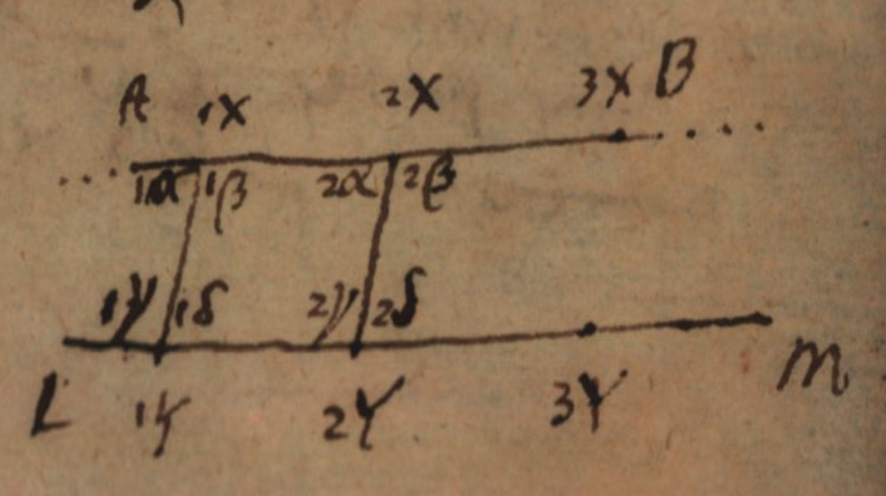
Soient les droites AE et LR et qu’un spectateur X soit transporté le long de celle-là, et un spectateur Y le long de celle-ci, tous les deux dans un mouvement uniforme, et les situations X ,Y, et la situation des spectateurs entre eux, tout autant que les droites indéfinies le long desquelles ils sont déplacés ne peuvent être distinguées entre elles. Au point que toutes deux ne sont pas seulement toujours semblables, mais aussi égales, et que les droites conformes (congruentia) seront parallèles. Mais il faut que la relation ne soit pas établie à partir de quelque point fixe, comme A ou L, sinon , en tout cas, la situation de l’une par rapport à l’autre peut être distinguée par l’avancée ou la régression par rapport au point fixe. Ainsi :si 1X2X=1Y2Y, nous avons 1X.1Y.X̅.Ȳ≃2X.2Y.X̅.Ȳ.
[…]
[Un long passage rayé]
Axiome: Si des choses semblablement déterminantes sont semblables, congrues, ou coïncidentes, celles qu’elles déterminent seront de même, et vice versa.
Si dans deux droites parallèles AB, LM sont découpées des droites égales 1X2X, 1Y2Y , du même côté (in easdem partes), et qu’elles soient reliées par les deux droites 1X1Y, 2X2Y ,le début de l’une au début de l’autre, la fin à la fin, toutes les droites seront égales entre elles. En effet puisque 1X.1Y.X̅.Ȳ≃2X.2Y.X̅.Ȳ on a 1X.1Y≃2X.2Y, et ainsi donc 1X1Y=2X2Y.

Les angles correspondants, que les droites de liaison ( jugentes) de la même droite font aux parallèles, sont les mêmes. En effet, si 1X1Y faisait un autre angle à a X̅, que 2X2Y, alors aussi (à cause de l’ axiome) 1X.1Y (dont ces deux points déterminent la droite) se comporteraient différemment envers X̅, que 2X.2Y, ce qui contredit le théorème ci-dessus, où l’on avait 1X.1Y.X̅≃2X.2Y.X̅.
Les droites passant par 1X, 1Y et par 2X, 2Y sont parallèles, en effet elles se comportent entre elles comme les droites [passant] par 1X, 2X, et par 1Y, 2Y, c’est-à-dire qu’un quadrilatère ayant les côtés opposés égaux, les a parallèles, ou encore est un parallélogramme.
Des parallèles sont dans un même plan. En effet, posés de la même façon, le plan 1Y1X.X̅ est le même que le plan 2Y2X.X̅ , sinon la première situation pourrait être distinguée de la dernière. Et ainsi, 1Y1X et 2Y2X (parallèles) sont dans le même plan que la droite X̅. On montrera de la même façon, que 1Y1X et 2Y2X sont dans le même plan que la droite Ȳ, et donc les droites X̅ et Ȳ sont dans le même plan.
Autrement si une droite est donnée, ainsi qu’un point qui n’est pas sur elle, il sera donné un plan commun à la droite et au point. Ce point sera dans l’un des deux segments du plan que la droite détermine. Ainsi, la droite parallèle passant par ce point sera dans le même plan, puisque quelque soit le point, il sera sur la droite, en tant que point.
La parallèle à une droite donnée passant par un point donné est unique. Parce que, étant donné un point par sa situation par rapport à une droite donnée et une partie du plan, un autre point est donné aussi parmi les autres points de la droite situés entre eux de la même façon. Et deux points étant donnés, la droite est donnée.
Soit la droite donnée Ȳ, le point donné C, et soit C.Ȳ≃X.Ȳ , X̅ sera une autre droite parallèle à la première droite passant par C.