Manuscripts on Fundamenta Calculi
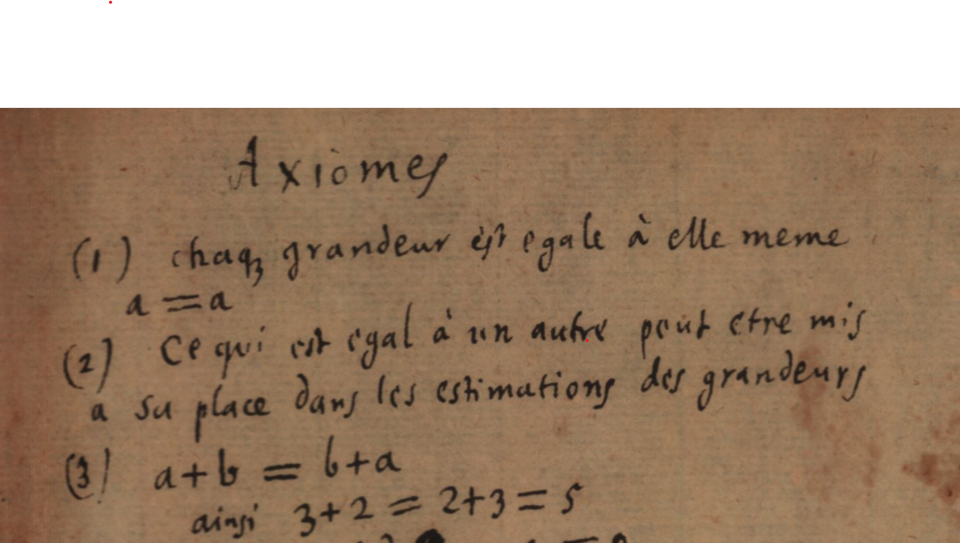
In this section, we present a series of texts dedicated to the axiomatic foundations of algebra. At first sight, it may seem that it was a topic that had interested Leibniz for many years, due in particular to his early interest in the building of abstract forms of calculi. A closer look at the manuscripts however, tends to indicate that this work on “foundations” (fundamenta calculi is one of the terms used by him) was typical of a late period. It appears to have started, to be more precise, in the wake of a treatise on mathesis universalis which Leibniz undertook in the spring of 1699 (on the context of this project, see Leibniz (2018), texts [3] and [4]) and which he wanted to complement by some rigorous “proofs” (see, in particular, the letter to Johann Andreas Schmidt from 3(13) March 1699 (A I, 16, 633), where Leibniz announces a treatise on fundamenta calculi following what he has already sent on mathesis universalis).
This goes against a common belief according to which Leibniz – like English algebraists in the 19th century – would have passed smoothly from the axiomatization of basic algebra (on numbers and magnitudes) to more “abstract” calculi, such as those he devised for logic in the middle of the 1680s (calculus de continente et contento or calculus coincidentium). Interestingly enough, the process seems to have been the other way round: the axiomatization of logical calculi made him aware of the problems raised by the axiom of idempotence, which does not hold in the usual treatment of magnitudes and of the subsequent impossibility of building a genuine “universal” calculus – as he had first dreamt. This could have motivated the wish to render the axioms of the calculus magnitudinum explicit – maybe in the hope of extracting a more abstract structure holding for all mathematical calculi (see the characterization of ars combinatoria in A VI, 4, 510 or 922-923). Another motivation, as explained in several texts from the beginning of the 1690s, came from physics, and more precisely from the formalization of Dynamica. Indeed, the “estimation” of forces necessitated enlarging the mathematical treatment of magnitudes so that “intensive” quantities could be dealt with. By contrast this forced, once again, the necessity of characterizing explicitly the particularities of the usual (or “ordinary”) calculus on magnitudes (See Leibniz 2018, text [3a] where the philosopher explains how he was led to return to the foundations of the treatment of magnitudes because he had to clarify the use of ratios and proportions in the realm of physics).
The first attempt in the axiomatization of algebra is the much celebrated text: Prima magnitudinum calculi elementa, which was edited by Gerhardt at the end of the 19th century and for which we now possess a precise date (see the presentation). This text is very similar to another entitled Mathesis generalis. An interesting difference between the two is that the latter tries to provide a foundation for natural numbers too – an enterprise for which we also possess the draft Numerus integer est totum ex unitatibus collectum (LH 35 I 9 Bl. 7). Yet it is important to keep in view that in this group of texts the central concept remains that of “magnitude” (and not that of “number”). The famous “analytical” proof of “2 + 2 = 4” from definitions (and an axiom of identity), which Frege took as a prototype of a logical view on numbers, takes place, in fact, in this context, where “number” is something needed for the measurement of magnitudes (and not a logical entity given a priori). The texts on the “Elémens du calcul”, written in French, are in the same spirit, but were written later (between 1707 and 1710, considering the type of paper used by Leibniz).
[LH 35 IV 13 Bl. 1-6] Prima calculi magnitudinum elementa : Overview | Translation | Transcription | See Original
[LH 35 I 9 Bl. 9-14] Mathesis generalis : Overview | Translation | Transcription | See Original
[LH 35 I 9 Bl. 7] Numerus integer est totum ex unitatibus collectum : Overview | Translation | Transcription | See Original
[LH 35 IV 12 Bl. 1-2] Elemens du calcul : Overview | Transcription | See Original