See a translation for the manuscript
Overview of Cum prodiisset (>1702)
The Cum Prodiisset manuscript was first published by Gerhardt, with no indication of its date and a few transcription errors [Leibniz,1846]. Child proposed an English translation in 1920 [Child, 1920, pp. 144-158]. He dated the manuscript from the time of the controversy with Bernard Nieuwentijt (1694-1695). This dating is not satisfactory since at the beginning of the text, Leibniz refers to the article by Thomas Gouye published in the Journal des Sçavans in May 1701 [Gouye 1701] and then to Hermann’s answer to Nieuwentijt [Hermann, 1700]. Additional evidence suggests that Cum Prodiisset is, in fact; intimately related to the twin texts presented in this section : Justification du Calcul des infinitésimales par celuy de l’Algèbre ordinaire and Defense du calcul des différences. Its date would thus be after 1702.
In Defense du calcul des différences, Leibniz announces that it is possible to offer two additional ways to justify his calculus, besides that grounded on the Lemmas on Incomparables and arguments in the manner of the Ancients. The first is a justification “by the ordinary calculus of Algebra” that is based on the principle of continuity. Leibniz expressly chooses a geometric configuration that appears intractable by using ordinary algebra (involving the quotient of two zeros). This example and the reasoning behind it are the same as those developed in Justification. The second way consists in giving an “interpretation” (interprétation is Leibniz’s word) of the computational process in which “very small magnitudes” (très petites grandeurs) are used instead of infinitesimals. Leibniz claims that this interpretation sheds more light on the reason why he spoke of “incomparables” (incomparables) in other places. However, the latter point is not developed here as the text ends with an uncompleted sentence: “En voicy un essay.” This second approach, involving “very small magnitudes”, reminds one of the strategy developed in the Cum Prodiisset. Indeed, in marginalia of this last text (neither reproduced nor translated by Child), Leibniz wrote
“all this must be edited very carefully so it can be published, omitting what is harsher in contradicting others. It is to be joined by my method for showing the law of continuity by the move of lines, in conformity with the tract [schediasma] I sent the Parisians in order to show that in the common example the ratio between nothings is feigned to be something”
It is possible to conceive of the Defense as one such attempt in which Leibniz intended to put together both the Justification, the only known schediasma sent to his Parisians in which the ratio of two hypothetic zeros is considered, and the Cum Prodiisset, the only known text where he implements a method based on “very small magnitudes.” [Rabouin & Arthur 2020].
Leibniz often argued that the rules of his calculus may be demonstrated by Archimedes-style arguments and the use of The Lemmas on Incomparables [AIII 7, 235, 576, 618, 857 ; AIII 8, 91], but by his own admission he never provided such a proof. In Cum Prodiisset, he does not do so either, but he presents two ways of justifying his calculus. One is based explicitly on the principle of continuity, while the other involves “finite witnesses” and avoids the use of infinitely small or vanishing quantities.
Leibniz prefaces his first method with a commentary on the principle of continuity. He had already formulated this principle (which he calls a postulatum) in other writings. The formulation in our text is the following: “in any proposed continuous transition ending in a terminus, one may institute a common reasoning in which the ultimate terminus is included”.
Reasoning based on this principle, he argues, is not new. He himself established results in geometry and other fields by drawing on it. In physics, for example, this principle allowed him to highlight errors that derived from applying Descartes’ and Malebranche’s rules for motion. He also points out that establishing results through arguments based on the principle of continuity is in fact common practice among other authors. Descartes recognized such a practice among the Ancients, which he referred to as “metaphysics of geometry”. Leibniz goes further and interprets the way some of his contemporaries (he cites Descartes, Christiaan Huygens and Philippe de La Hire) establish results as also falling within this type of reasoning. There are many well-known examples of the application of this principle — what can be said of a polygon can be said of a polygon with an infinitely-sided polygon, that is to say a curve; what applies to an ellipse applies to an ellipse whose focus is at infinity, i.e. a parabola, etc. It must be stressed, however, that Leibniz was the first to explicitly formulate this principle.
How does he use this principle to present his first method?
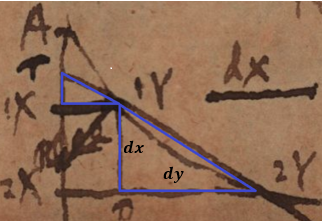
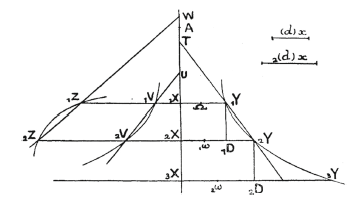
He presents his method by applying it directly to determining the tangents of the common parabola and the cubic of equation x ^ 3= aay. His method relies on a geometric configuration, usual at the time, consisting of two similar triangles, one formed by the subsecant T1X and the ordinate T1Y (Leibniz indicates indices by a number before the letter) and the other formed by the differences dy and dx . His purpose is to establish a general expression for \frac{dy}{dx}. Leibniz calls this expression a “general rule” [regula generalis], and then appeals to the principle of continuity: the reasoning is valid for the extreme case where the ordinate 2X2Y moves until it is very close to the fixed ordinate 1X1Y. In this case, the differences can be considered to be infinitely small and the secant T1Y is the tangent. He therefore allows himself to use that dx = 0 to obtain the expression of \frac{dy}{dx} corresponding to the tangent. Leibniz takes up the idea developed in the example of Justification, also taken up in Defense, in which a ratio between two vanishing quantities is always interpretable even as they vanish because it is equal to a proportion between two finite quantities.
This last reasoning involves infinitesimals which make it possible to imagine the case where the differences are zero as if they were not. However, Leibniz, probably anticipating criticisms, points out that it is quite possible to obtain the same computational results by considering that the differences are not evanescent but arbitrarily small finite quantities. The key to his method lies in the introduction of a segment which is finite and constant, denoted (d)x. In Nova Methodus, Leibniz had also introduced a finite segment to present his calculus, probably with a view to excluding other presentations involving infinitely small quantities [Hess 1984]. However, in Cum Prodiisset he took fuller advantage of this idea. He considers a segment (d) y such that (d) y: (d) x = dy: dx = 1XT: 1X1Y . The segment (d) y is finite, its trivial construction depends on dx . For any other curve VV with the same axis as YY with 1X1V = v and 1X1V = v + dv , he also considers (d) v such that (d) v: (d) x = dv: dx = 1XU: 1X1U . The triangles with sides dx and dy or dx and dv ,… are each similar to a finite “witness” triangle.
figure geogebra
Leibniz demonstrates the differentiation rules for finite quantities (d) x, (d) y, (d) v which are valid even in the case where the triangles (of sides dx, dy, dv, …) vanish since the similarity is supposed to remain. He points out that this reasoning could be imagined [fingendo] by using unassignable quantities since their ratio would be the same as that of finite and real quantities. As pointed out by Rabouin and Arthur, Leibniz’s procedure facilitates Archimedian-style demonstration. Here, obtaining this type of equality would be conducive to an Archimedean demonstration of the rules of the calculus [Rabouin & Arthur 2020].
Leibniz similarly demonstrates the rules of second-order differentiation even if, as Bos showed in a seminal article which did much for the fame of our text [Bos 1974], his reasoning is insufficient. Indeed, Leibniz assumes without making it explicit that the differential of one variable is constant [Bos 1974, 59-62].