See a transcription for the manuscript
Overview of Defense du calcul des Differences (1702)
Defense du calcul des Differences is clearly to be situated at the same time and in the same context as Justification du Calcul des infinitésimales par celuy de l’Algèbre ordinaire which we also present in this section (available here). While the notation is different, their developments are based on identical geometric configuration.
It is possible that Leibniz wrote Justification first and then used it later to write a longer text in which he kept the same example. Indeed, although very similar, Defense du calcul des Differences, unlike Justification, contains a preamble in which Leibniz announces his intention to show that in his calculus the elisions of infinitely small quantities are not made in an arbitrary manner as argued by “des personnes habiles qui s’opposent au Calcul des Différences” but according to rules that can be justified in the manner of Archimedes. These rules are based on his famous Lemmas on Incomparables [Leibniz, 1689] whose application makes it possible “to know what can be neglected with impunity without it being able to cause any error”.
By invoking the “des personnes habiles qui s’opposent au Calcul“, Leibniz was addressing academicians like Rolle and Galloys, who refused to recognize the exactness of differential calculus.
Leibniz had already addressed a justification of his calculus to the French savants. A year earlier, in a short article in the Journal de Trévoux [Leibniz 1701b], he explained that the practice of his calculus does not require taking the infinitely small in a “rigorous” manner but as quantities as small as needed. Taking the same comparison with finite magnitudes as he did in his inaugural article presenting the Lemmas on Incomparables [Leibniz 1689] (the diameter of a grain of sand, the diameter of the Earth and the distance from the fixed stars), he caused confusion amongst the members of the Académie des sciences, both opponents and defenders of differential calculus alike. This intervention was followed by an article in the Journal des Sçavans [Leibniz 1702] in which he clarified what he meant by “to explain the infinite by the incomparable” [expliquer l’infini par lincomparable] and how differentials could be considered as “ideas suitable for abbreviating reasoning, and grounded in reality” [des idées propres à abréger les raisonnemens, & fondées en realitez].
In Defense du calcul des différences, Leibniz announces that it is possible to propose two other ways of justifying his calculus (in addition of the one that based on the Lemmas on Incomparables and reasoning in the manner of the Ancients). The first is a methodological justification “by the ordinary calculus of Algebra” and which is based on the principle of continuity. His reasoning is the same as that developed in Justification. The second is an interpretation of the computational process: considering “very small quantities” instead of infinitesimals. Leibniz claims this would shed more light on what made him speak of incomparables in other times. However, this last point is not developed here since its text ends leaving “En voicy un essay” pending. This last strategy brings to mind that developed in the Cum Prodiisset [Leibniz 1702b]. In marginalia of this last text, Leibniz wrote “all this must be edited very carefully so it could be published, omitting what is harsher in contradicting others. It is to be joined by my method for the law of continuity shown by the tracing of lines, and also by the tract [schediasma] I sent the Parisians in order to show that in the common example the ratio between nothings is feigned to be something” (translate in [Rabouin & Arthur 2020]). It is therefore possible that the Defense is an attempt in which Leibniz intended to bring together both the Justification (the only known schediasma sent to Parisians) and the Cum Prodiisset (the only known text where he implements a method based on “finite witnesses”) [Rabouin & Arthur 2020].
By “justifying our way of calculating by that of ordinary Algebra”, Leibniz wants to make it clear that those who practice the ordinary calculus of algebra, already use infinitely small quantities even if some of them claim that these quantities are in fact zero. Presenting his calculus, criticized in such a vivid manner by the algebraists, as based on the very same foundations as those they need for their own practice, Leibniz adopts a new strategy of justification, different from the one he had developed a few months earlier.
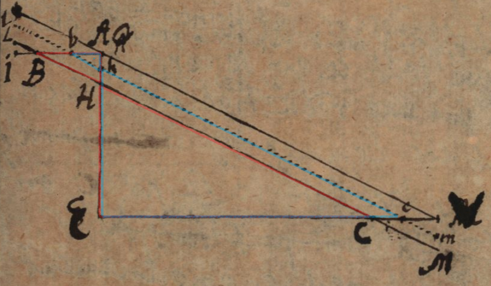
This second justification, in support of geometrical configuration, is practically the same as that of Justification. To understand this geometrical situation using calculus in all its generality, that is to say until the triangle vanishes completely, it must be accepted that the lengths of the sides never become absolutely zero, but that ‘”at the last moment” they are infinitesimal. Thus, thanks to the Law of Continuity, they keep among themselves the essential property of magnitudes which is to have a ratio. It is the existence of this “last ratio” that allows us to understand the geometrical situation in all its generality.