See a transcription for the manuscript
Translation of Quaestio de Jure
La question [qui consiste à déterminer] de quel droit on peut négliger les quantités infiniment petites en comparaison des ordinaires ou les ordinaires au regard des infinies ; et des infinitésimales (infinitesimas) quelconques[de quelque ordre qu’elles soient] au regard de celles qui leur sont infinituples, a suscité récemment beaucoup de disputes à l’Académie des Sciences, et cette affaire a conduit à ce que certains requièrent aussi mon jugement. La chose me semble se ramener à ceci : il faut œuvrer à ce que la Mathesis pure soit préservée dans son intégrité des controverses métaphysiques. C’est ce que nous ferons si nous nous soucions peu de savoir si sont réels les infinis et infiniment petits dans les quantités, les nombres, les lignes ; que l’on utilise donc les infinis et infiniment petits comme une expression apte à ramasser des pensées. Ainsi est-il permis qu’elles soient imaginaires. [Et] que ces quantités puissent cependant être employées à la manière des racines imaginaires en Algèbre.
D’où il s’ensuit qu’il ne faut jamais utiliser cet abrégé sans qu’une explication ne lui soit substituée, par laquelle la chose sera ramenée à une démonstration rigoureuse à la façon d’Euclide ou d’Archimède. Et ceci de la façon que j’ai donnée dans les Acta Eruditorum, quand j’ai expliqué les Lemmes des Incomparables. En effet on peut dire que se comportent ainsi les divers degrés d’infinis ou d’infiniment petits, à la manière dont je conçois que la distance des étoiles fixes est incomparablement plus grande que le diamètre du globe terrestre, et ce globe [incomparablement plus grand] qu’un grain de sable ; et le grain de sable [incomparablement plus grand] qu’un corpuscule de lumière de sorte que l’un soit tenu pour un point en comparaison de l’autre. Même si aucune quantité déterminée de cette sorte n’est employée dans notre Méthode, mais seulement [une quantité] aussi petite que l’on veut. Lorsque donc, on peut montrer dans les affirmations des Géomètres qu’une erreur est plus petite que toute assignable, c’est-à-dire qu’elle est nulle ; nous disons pour abréger que l’erreur ou l’écart est infiniment petit et nous l’emploierons dans le calcul comme une quantité et la négligerons en comparaison de ce dont elle s’écarte. Puisque aussitôt le raisonnement devient rigoureux, lorsque l’on échange l’indéfiniment petit avec un petit déterminé, mais que la démonstration montre que ce dernier peut être rendu moindre qu’une quantité assignée, ce qui peut être tenu pour nul, de sorte que la chose se ramène en quelque façon à ce genre particulier de démonstration, dont on trouve des exemples un peu partout, dans laquelle à partir de l’inégalité supposée de deux quantités nous concluons directement à leur égalité.
Et ceci est le principe du calcul différentiel, quand nous supposons que des écarts ou différences sont incomparablement moindres que ces mêmes différences, et que nous reconnaissons alors divers degrés, constituant une certaine loi des homogènes d’un genre nouveau.
Et ces quantités indéfinies sont utiles, aussi pour les propositions universelles à propos des [quantités] déterminées. Par exemple les théorèmes sur les droites concourantes sont vérifiés pour les parallèles [prises] comme une espèce des convergentes, lorsque le point de concours est éloigné à l’infini. Ainsi tout ce qui est démontré pour les Ellipses est vérifié aussi pour la Parabole d’une façon certaine, si l’on conçoit la parabole comme une Ellipse dont l’un des foyers est infiniment éloigné.
De là nait cette Loi de Continuité dont j’ai montré il y a quelque temps la grande utilité en physique dans les Nouvelles de la République des Lettres. Par où il faut concevoir l’égal comme un inégal évanouissant, et le repos comme un mouvement infiniment petit ; et ce même genre [de choses] ailleurs. Où lorsque l’une des données s’évanouit dans l’autre, comme le mouvement dans le repos ; ainsi la règle pour le mouvement doit s’évanouir dans la règle pour le repos dans les mêmes circonstances. Autrement les règles sont incohérentes.
C’est pourquoi il faut admirer partout où il se produit l’artifice de la nature, selon lequel toutes choses procèdent donc dans le calcul comme si ces quantités étaient réelles au plus haut point ; Et, sans cela, l’ordre et connexion des choses ne peut subsister.
En ce qui concerne quelques difficultés provenant des séries infinies, je dis qu’à proprement parler, il ne faut pas opposer le rien à l’infini, mais qu’il faut opposer le rien au tout et l’infini petit à l’infini. En effet, \frac{1}{0} = infini n’est pas une vraie proposition, sauf si 0 signifie un nombre infiniment petit, qui peut être assurément abandonné en tant que succédané de ce même 0, pour les rapports susdits, comme si je disais \frac{aa}{dx} = f , donc la quantité ordinaire a est moyenne proportionnelle entre l’infinie f et l’infiniment petite dx.
Par conséquent, il ne faut pas penser que deux fois 0 sera autre chose que 0, comme j’ai appris que certains hommes ingénieux l’ont affirmé, confondant d’une certaine manière l’infiniment petit et le nul.
Quand on étudie les séries infinies par division ou extraction, ou par d’autres moyens, la force de la vérité consiste en ceci que l’on montre l’écart plus petit qu’une quantité quelconque. Ainsi, si quelqu’un disait qu’il y a un écart entre le cercle, et cette quantité trouvée par moi 1 -\frac13 + \frac15 - \frac17 + \frac19-\frac{1}{11} etc. (le carré du diamètre étant posé [égal à] 1) : je montrerai que cet écart est nul, c’est-à-dire plus petit que tout ce qu’il pourra assigner. Parce que dans cette série où que tu t’arrêtes de progresser, l’erreur est toujours inférieure à la fraction immédiatement suivante, et à coup sûr, si on progresse assez, elle est inférieure à une quantité toute quantité donnée, quelle qu’elle soit.
Voilà pourquoi la division continuée ne donne pas une série de fractions égales, si ce n’est quand les termes décroissent. Car pour que l’erreur puisse être montrée inférieure au donné, il faut que la série soit décroissante, et même suffisamment [décroissante].
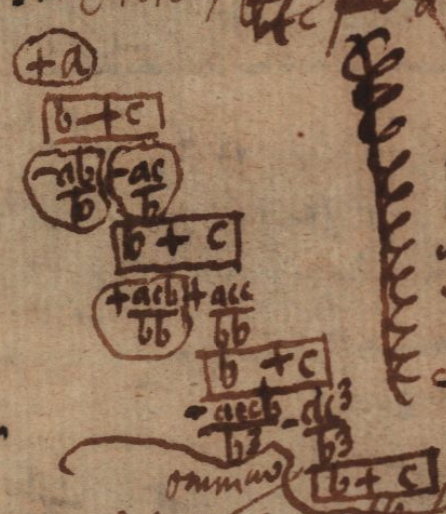
Ainsi dans la fraction \frac{a}{b + c}, si tu divises a par b+c il vient
ʄ \frac{a}{b} - \frac{ac}{bb} + \frac{acc}{b^3} - \frac{ac^3:b^3}{b + c} (ʄ [facit])
de sorte qu’il soit permis d’arrêter où l’on veut, pour autant que dans le dernier reste, ici - ac^3 : b^3, l’on doive mettre sous le trait [de fraction] b+c, pour qu’apparaisse la fraction : \frac{-ac^3 : b^3}{b+c}, qui, ajoutée à la série, la rende égale à la fraction donnée \frac{a}{b + c}.
Ainsi si on a \frac{a}{b + c} = \frac{4}{3 + 1} = \frac{4}{4} = 1 cela donnera \frac43 - \frac49 + \frac{4}{27} - \frac{4 :27}{3 + 1}, c’est-à-dire \frac43 - \frac49 + \frac{4}{27} - \frac{1}{27} = \frac43 - \frac49 + \frac{3}{27} = \frac43 - \frac49 + \frac19 = \frac43 - \frac39 = \frac43 - \frac13 = 1.
Et où que tu continues la série, on aura \frac43 - \frac49 + \frac{4}{27} - \frac{4}{81} etc. jusqu’à \pm (+ ou -) \frac{4}{3 + 1} \frac{1}{3^e} qui peut être rendu inférieur à toute [valeur] donnée. Mais si on avait \frac{4}{1 + 1}, où tu t’arrêteras, il restera toujours (+ ou -) \frac{4}{1 + 1} \frac{1}{1^e} mais \frac{1}{1^e} = 1, donc il reste toujours \frac{4}{2} qui ne décroit pas et ne peut devenir inférieur à toute donnée.
Ceci s’étend donc à une série telle que \frac{2}{2 - 2} = 1 + 1 + 1 + 1 etc. = \frac20 ou à celle telle que \frac{2}{1 - 1} = 2 + 2 + 2 + 2 etc. = = \frac20, qui devraient être égales entre elles alors que l’une est double de l’autre ; il faut dire qu’ici il n’y a nulle égalité entre la série infinie et la fraction. Aussi, il ne faut pas dire du absolument rien, ni qu’on divise, ni qu’on multiplie, si ce n’est pour l’enlever totalement. Mais cet \frac10, 0 étant posé pour le néant parfait, doit être absolu, c’est-à-dire une infinité dont il n’existe aucune extension, ou même quantité. Or cet absolument infini, à savoir Dieu en quantité calculable, est privé de parties assurément et l’ensemble des choses (τò omnia) qui possède des parties, n’est pas un vrai tout, c’est-à-dire ne peut constituer une quantité qui peut être changée par multiplication ou division.
De même il faut répondre de cette façon à celui qui, supposant 0 comme une quantité, et utilisant ces deux axiomes acceptés, (primo) des égaux à un troisième sont égaux entre eux, et (2do) des égaux multipliés ou divisés par la même quantité restent égaux, – sans référence à notre calcul infinitésimal – argumentera comme suit : 1, 0 = 0 = 2 − 2 = 2, 1 – 1 = 2, 0. Donc 1, 0 = 2, 0 donc 1 = 2, ce qui est absurde.
Il faut répondre que le vrai 0, c’est-à-dire pris comme absolu, ne peut être soumis à un tel calcul, c’est-à-dire que si quelque chose est multiplié par 0, et le produit à nouveau divisé par 0, il n’est pas restauré, parce que n’importe quoi multiplié par 0 donnera la même chose, à savoir rien.
Et tu insisteras qu’à tout le moins, on peut montrer que \frac10 = \frac20, c’est-à-dire que quelque chose est double de lui-même car \frac10 = \frac{1}{1 - 1} = \frac{2}{2 - 2} = \frac20. Il faut répondre que \frac10 ne peut être soumis à un tel calcul, c’est-à-dire que \frac10 n’est pas doublé quand on le multiplie par 2, ce qui fait qu’il n’est pas permis de dire deux fois \frac10, si ce n’est de la même façon que nous disons deux fois la même chose ajoutant ainsi rien [nihil] comme lorsque nous répétons la même vérité, puisque \frac10 signifie l’opposé de rien, c’est-à-dire l’ensemble de toutes les choses [omnia], le Nombre de toutes les unités. Et si quelque chose multiplie l’ensemble de toutes les choses, elle ne produira rien de nouveau, puisque l’ensemble de toutes les choses ne peuvent être augmentées. Comme si on divise le rien par quelque nombre, soit en deux, trois etc. parties, il ne produira rien de nouveau, parce que le rien ne peut être diminué. En retour, puisque le rien ne peut être doublé, il ne peut pas être supposé la moitié du nombre de toutes les choses, c’est-à-dire du nombre de toutes les unités, à partir de ces choses on comprend que le rien et toutes les choses ne sont pas changés en multipliant et divisant. Mais il en va autrement de la supposition de l’infini et des infiniment petits, dont nous nous servons dans le calcul, c’est-à-dire du aussi petit ou de l’aussi grand qu’il faut pour que l’erreur soit montrée inférieure qu’un donné.