Transcription of Trigonometria Sphaerica Tractanda per Projectionem in Plano (1679 – 1680)
⟨Tri⟩gonometria sphaerica tractanda per projectionem in plano
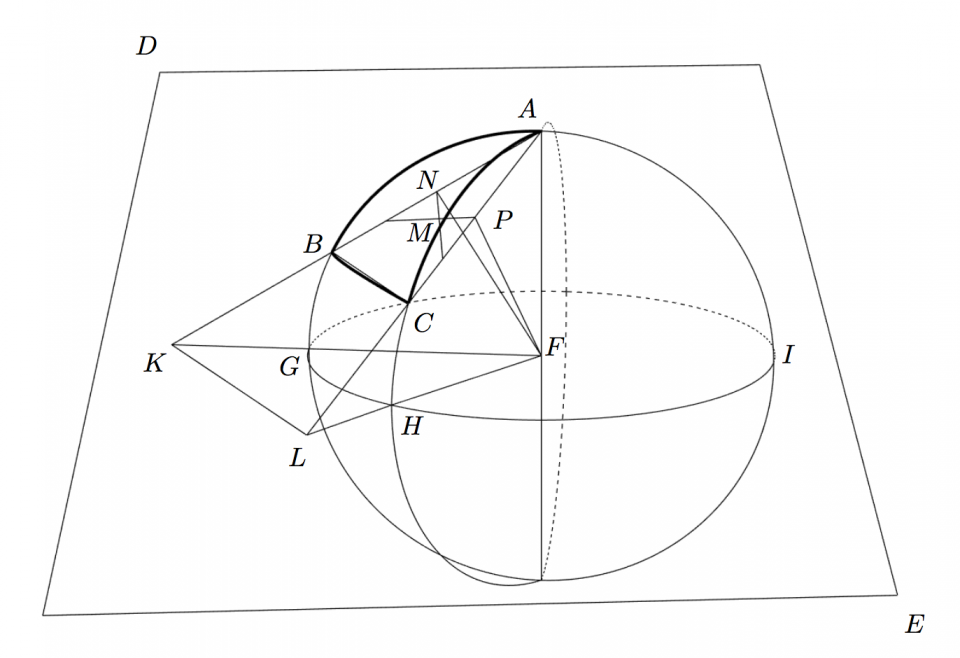
Sit Triangulum Sphaericum ABC, et planum DE secans sphaeram in tribus punctis A. B. C. utique projectio trianguli sphaerici ABC, erit triangulum rectilineum ABC in plano DE descriptum, cujus latera se habebunt ad latera sphaerici, ut chordae se habent ad suos arcus, radio FA. FB. FC, ex centro sphaerae F semper existente eodem. Jam quia et angulos trianguli sphaerici quodammodo in plano exhibere volumus, hinc polo A describatur aequator GHI arcus AB, AC productos si opus secans in punctis G et H.
[On the side:]


[End]
Quoniam ergo omnis projectio circuli magni in plano, si ex sphaerae centro spectetur, est recta, hinc arcus aequatoris, GH projectio in plano DE, sit recta KL. In plano DE jungantur puncta A et K, recta AK transibit per B. et AL eodem modo per C.
A puncto F (sphaerae centro) ad planum DE, vel ABC ducatur minima, quae hoc loco cadet intra triangulum ABC, quia cum sit minor quam FA vel FB vel FC, erit intra sphaeram, sola autem plani DE, portio ABC est intra sphaeram. Methodus a dato puncto F ad datum planum ABC ducendi FM lineam minimam posito tria plani puncta A. B. C, esse data, eorumque distantiam a puncto extra planum a quo minima quaeritur; esse etiam datam, talis erit. Datis trianguli ABF tribus lateribus AF. AB. FB, dabitur altitudo FN, minima a puncto F, ad rectam AB, ergo dabitur et AN, ergo et punctum N, ex quo educatur perpendicularis NM, angulo MNA vel MNB recto.
[On the side:]
[End]
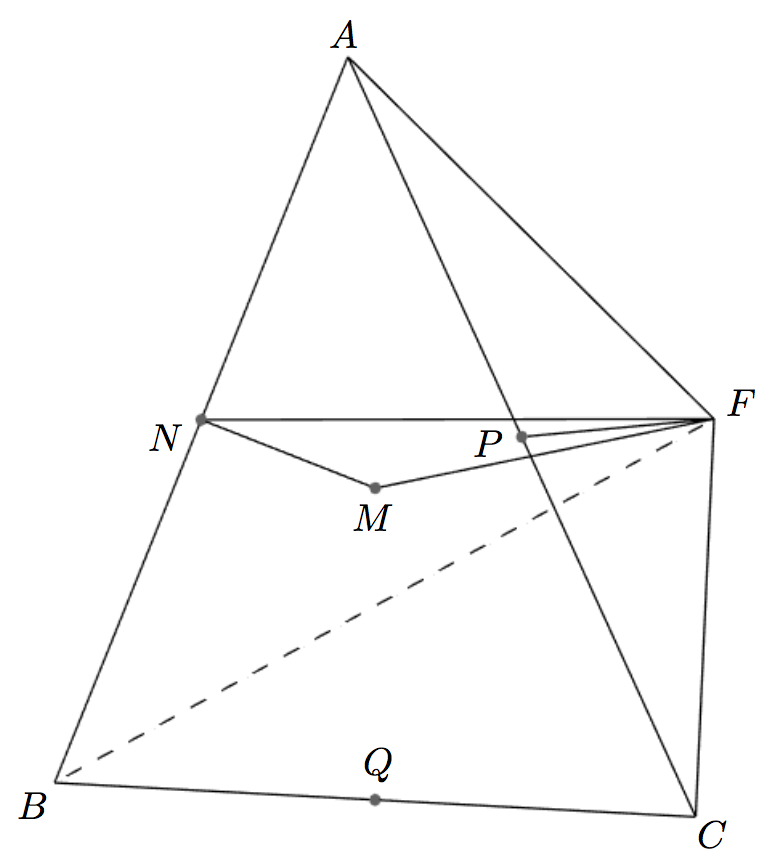
Eodem modo investigetur punctum P in recta AC, respondens ipsi N in recta AB, ex quo puncto P educatur etiam perpendiculariter PM, angulo MPA vel MPC recto, quae duae perpendiculares se secabunt in puncto M, et FM, erit Minima, quia MN minima ex M ad AB, et FN minima ex F ad AB, ergo et summa quadratorum ab FN et MN, hoc modo minima, ergo et FM latus hujus summae minima. Ubi notandum si ea methodo qua N et P investigetur Q, in recta BC, et inde educatur normalis, ad BC, eam etiam incidere in punctum M.
Hoc loco autem, cum puncta A. B. C. aequidistent a puncto F, puncta N. P. Q. erunt media rectarum AB. AC. BC. et punctum M, erit centrum Circuli triangulo ABC circumscripti. (Habetur AG diagonalis quadrati ab AF. (Habetur et BG chorda arcus BG.) Sed non opus puncto M. Nam cum angulus GFA vel KFA sit rectus, et sumto puncto N medio ipsius AB, junctaque FN sit angulus FNA rectus, erunt triangula AFK et ANF similia, et cum dentur AF, AN (seu \dfrac{1}{2}AB), FN[/latex], ideo dabuntur et AK, KF.
Nimirum AK : AF :: AF : AN. Seu AK aequ. : AF^2\smile+\dfrac{1}{2}AB. Eodem modo AL aequ. AF^2\smile+\dfrac{1}{2}AC. Ergo AK : AL :: AC : AB. Cumque AL et AK, itemque AB et AC, angulum comprehendant eundem in A, erunt triangula ABC, et ALK similia, et quod notabile sub-contraria. Itaque cum dentur AF. AB. AC. BC, erit \underline{AK} aequ. AF^2\smile+\dfrac{1}{2}AB, et de reliquo \underline{AL : AK : KL} :: AB : AC : BC.
Eodem modo habebimus et FL, nam sumto P puncto medio rectae AC jungamus FP, erit APF triangulum rectangulum simile ipsi AFL, ut supra Triang. ANF simile Triangulo AFK. Ergo habemus FK : AF :: NF : AN. seu FK aequ. AF, NF\smile\dfrac{1}{2} AB et FL[/latex] aequ. AF, NP\smile+\dfrac{1}{2}AC. Est autem NF aequ. \sqrt{AF^2–\dfrac{1}{4}AB^2}, et NP aequ. \sqrt{AF^2–\dfrac{1}{4}AC^2}. Ergo AB+\sqrt{AF^2–\dfrac{1}{4}AC^2}:AC\sqrt{AF^2–\dfrac{1}{4}AB^2}::FL:FK seu erit FL aequ. AF\sqrt{AF^2–\dfrac{1}{4}AC^2}\smile\dfrac{1}{2}AB. FK aequ. AF\sqrt{AF^2–\dfrac{1}{4}AB^2}\smile\dfrac{1}{2}AC. Et supra KL aequ. \dfrac{2BC.AF^2}{AB.AC}.
[On the side:] \dfrac{KL}{AL} \sqcap \dfrac{BC}{AB} [End]
Trianguli autem FKL idem est angulus ad F qui est angulus sphaericus BAC. Eodem modo et caeteros angulos sphaericos in plano poterimus exhibere uti iam ipsa latera Trianguli sphaerici in plano exhibuimus per suas chordas. Et omnia haec triangula consistent circa idem punctum F.
[At the end:]
KL\sqcap \dfrac{BC(AL)AF^2}{AB\dfrac{1}{2}AC} KL\sqcap \dfrac{2BC.AF^2}{AB.AC}

[End]
Trigonometria sphaerica projectione in planum explicata
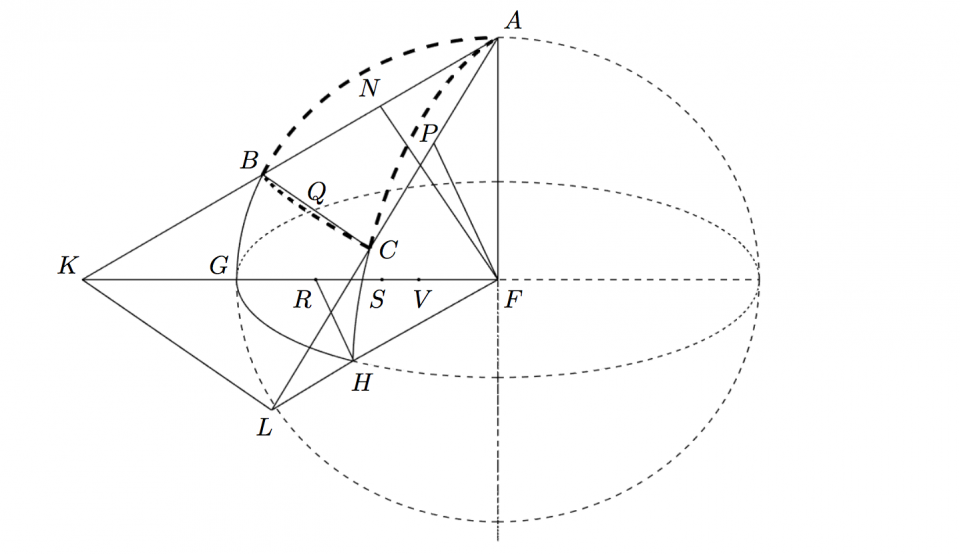
In Sphaera centro F, radio FA descripta, sit Triangulum Sphaericum (ex arcubus circulorum maximorum constans) ABC polo A, meridianorum quadrantibus ABG, ACH describatur arcus aequatoris GH. Et ducantur radii FG, FH aequales ipsi FA, et ad AF normales. Habemus duos quadrantes planos ABGF et ACHF, quorum angulus est idem qui rectarum GF, HF, unde arcus aequatoris GH erit mensura anguli duorum planorum, seu anguli sphaerici A.
Jungantur puncta A. B. C. rectis, et habebitur Triangulum rectilineum ABC quod erit communis sectio sphaerae, et plani per tria puncta A. B. C. transeuntis. Cum rectae AB, FG sint in eodem plano, sunt enim ambae in quadrante plano ABGF, productae convenient alicubi in puncto K (parallelae enim non sunt, quia angulus AB ad AF acutus, GF ad AF rectus) similiter AC et FH, cum sint in eodem plano, nempe in quadrante plano ACHF, convenient alicubi in L. In recta AB sumatur punctum medium N, et in AC medium P, et jungantur FN, FP, erunt anguli N et P recti. Ergo triangula rectangula similia ANF et AFK, item similia APF et AFL. Ergo AN : AF : NF :: AF : AK : FK. Similiter AP : AF : PF :: AF : AL : FL. Ergo AF media proportionalis inter AN et AK, item inter AP et AL. Ergo rectangulum NAK aequale rectangulo PAL, ac proinde et rectangulum BAK aequale rectangulo CAL. Ergo AB : AC :: AL : AK. Triangula ergo ABC, ALK angulum A communem habentia, et latera angulum A, comprehendentia, proportionalia; erunt similia, et quod notabile subcontraria.
Ex his si valores linearum rectarum quaeramus, erit AK aequ. AF^2\smile AN et AL aequ. AF^2\smile AP et KL aequ. BC.AL\smile AB vel quia BQ est \dfrac{1}{2}BC, et AN est \dfrac{1}{2}AB, erit KL aequ. BQ.Al\smile AN et pro AL substituendo valorem AF^2\smile AP fiet \underline{\underline{KL}} aequ. BQ.AF^2\smile \overline{AP.AN}. Seu KL ad sinum ipsius arcus BC, (Lateris Trianguli sphaerici) ut in composita ratione sinus totius ad sinus reliquorum laterum. KF^2 aequ. KF^2-AF^2. Ergo KF^2 aequ. AF^4-AF^2.AN^2, \smile AN^2 seu KF aequ. AF\sqrt{AF^2-AN^2}\smile AN. et LF^2 aequ. AL^2-AF^2. Ergo LF^2 aequ. AF^4-AF^2. AP^2, \smile AP^2 ergo erit LF aequ. AF\sqrt{AF^2-AP^2}\smile AP. \sqrt{AF^2-AN^2} est FN. et {AF^2-AP^2} est FP. Unde \underline{\underline{KF}} aequ. AF.FN\smile AN et \underline{\underline{LF}} aequ. AF.FP\smile AP. Unde valores KL.KF.LF conjungendo fiet: LF.FK\smile LK aequ. FN.FP\smile BQ. Quae theoremata omnia sunt elegantissima.
Et dato Triangulo ABC plano, seu sinibus laterum Trianguli sphaerici potest construi triangulum planum FKL habens angulum F eundem cum angulo trianguli sphaerici A. Idemque est de caeteris angulis sphaericis. Unde datis omnibus lateribus trianguli sphaerici habentur et anguli. Quae calculo prosequi operae pretium erit. Si jam addatur alibi a nobis aliisque demonstratum sinus laterum et sinus angulorum oppositorum esse proportionales cuncta eo facilius absolventur. Datis autem tribus lateribus: FL, FK, LK. angulus F ex communi Trigonometria ita invenitur: fiat ut duplum rectang. FL.FK ad differentiam inter FK^2+FL^2 et LK^2 ita sinus totus AF ad FR ad sinum complementi anguli GFH. (R autem rectus intelligi debet.) Per supra dicta LF.FK aequ. FN.FP.LK\smile BQ. Et LK\smile BK aequ. AF^2\smile AP.AN. Ergo LF.FK aequ. FN.FP.AF^2\smile AP.AN. \pm FK^2\pm FL^2\pm LK^2 aequ. \pm AF^2.FN^2\smile AN^2, \pm AF^2. FP^2\smile AP^2, \pm BQ^2.AF^4\smile AN^2.AP^2, seu aequ. \pm AF^2.FN^2.AP^2\pm AF^2.FP^2.AN^2\pm BQ^2.AF^4, \smile AN^2.AP^2. Sit sinus Totus FT. eritque FR : FT :: \pm FN^2.AP2\pm FP^2.AN2\pm FT^2.BQ2 : 2, FN.FP.AP.AN. Seu FR\smile FT aequ. \pm\dfrac{1}{2}.\pm\dfrac{FN.AP}{FP.AN}\pm\dfrac{1}{2} \dfrac{FP.AN}{FN.AP}\pm\dfrac{1}{2} \dfrac{FT^2.BQ^2}{FN.FP.AP.AN}. Sint
FR.FS.FV sinus compl. angulorum A. B. C. Pro FS loco A. B. N. P. C. Q ponetur B. A. N. Q. C. P. Pro FT loco A. B. N. P. C. Q ponetur C. A. P. Q. B. N. Ergo FS\smile FT aequ. :: \pm FN^2.BQ^2\pm FQ^2.BN^2\pm FT^2.AP : 2, FN.FQ.BQ.BN. Et FV\smile FT aequ. :: \pm FP^2.CQ^2+/-FQ^2.CP^2\pm FT^2.AN^2 : 2, FP.FQ.CQ.CP.
Sunt autem AN et BN, item AP et CP, item CQ et BQ aequales. Sinus scilicet recti arcuum AB, AC, BC, FN, FP; FQ sicut sinus complementi eorundem arcuum. Sinum rectum vel sinum compl. arcus AB. scribemus SrAB. ScAB et sinum complementi anguli A, scribemus: ScA. et ita valores ipsorum FR. FS. FV. Seu ScA. ScB. ScC denuo scribemus
\dfrac{2ScA}{rad} aequ. \pm\dfrac{ScAB}{SrAB}.\dfrac{SrAC}{ScAC}\pm\dfrac{ScAC}{SrAC}.\dfrac{SrAB}{ScAB} \pm\dfrac{rad^2.\overline{SrBC^2}}{SrAB.ScAB.SrAC.ScAC}
\dfrac{2ScB}{rad} aequ. \pm\dfrac{ScAB}{SrAB}.\dfrac{SrBC}{ScBC}\pm\dfrac{ScBC}{SrBC}.\dfrac{SrAB}{ScAB}\pm \dfrac{rad^2.\overline{SrAC}}{SrAB.ScAB.SrBC.ScBC}
[On the side:]
Sc. sinus compl. Anguli A
Sc.AB sinus compl. Arcus AB
Sr.AB sinus rectus Arcus AB
Radius. rad
[End]