Transcription of Constructor (1674)
Inveni mense Xbri 1674. Parisiis
Godofredus Guilielmus Leibnitius
C o n s t r u c t o r
Instrumentum Algebraicum
pro inveniendis omnium Aequationium Radicibus, 10
geometrice pariter, et in numeris quantumlibet exactis
sine calculo.
Descriptio C o n s t r u c t o r i s sive Instrumenti Algebraici
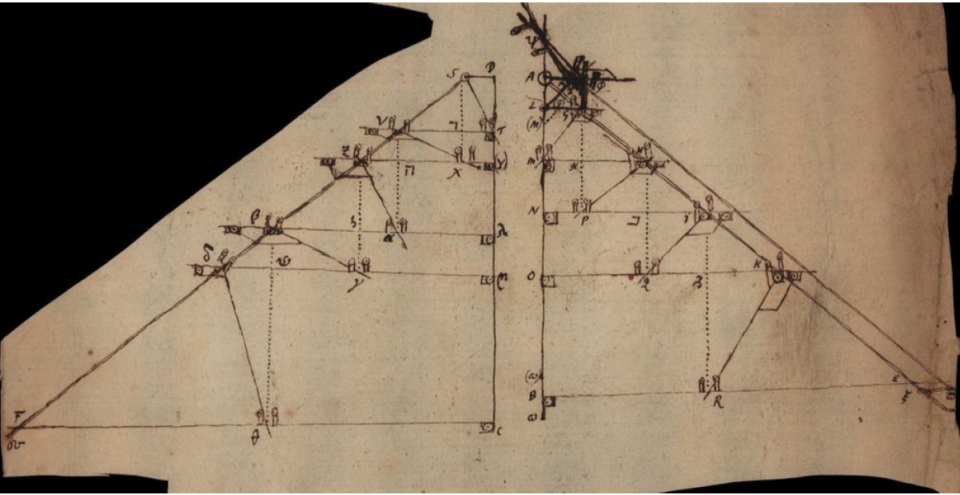
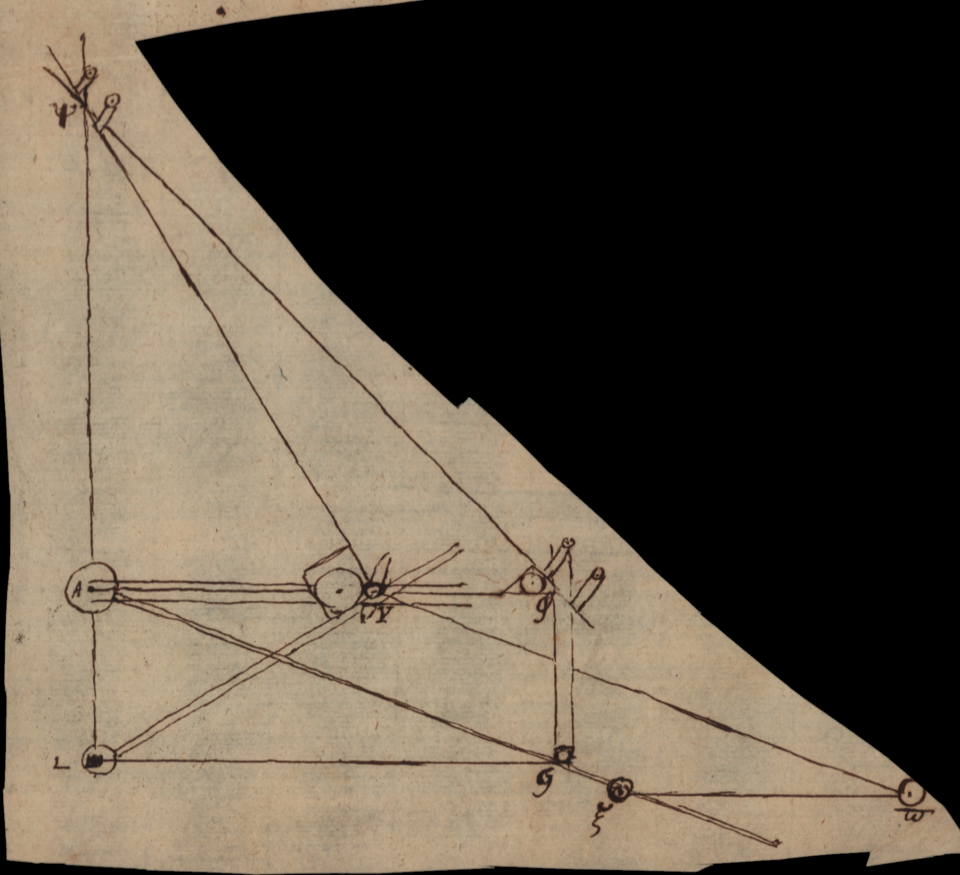
In plano hujus paginae figurae 1 rectangulum paginae parallelum ABCD designatum intelligatur et super rectis AB, DC, perpendiculariter erecta plana, ABE, et DCF, sibi proinde parallela. Punctum A summum, B imum, E dextrum, C sinistrum.
Ex puncto A ducatur dextrorsum simul ac deorsum recta AGHIKE. secans rectas indefinite dextrorsum productas ipsi ALMNOB perpendiculares LG, MH, NI, OK. Sint indefinite deorsum productae GP, HQ, IR perpendiculariter secantes ipsas NPI, OQK, BRE; junctaeque transversales GM, HP, IQ, KR indefinite deorsum pariter et sinistrorsum productae. Ipsae AL, LM, MN, NO, OB, sumtae prout e re erit. Intelligantur jam rectae quidem AB et LG esse lineae rigidae impraesentiarum immobiles, sed MH, NI, OK, sint regulae mobiles sursum ac deorsum in ipsa AB, et GM, HP, IQ, KR dextrorsum et sinistrorsum in rectis GL, HM, IN, KO, EB, ita tamen ut durante motu tam priores quam posteriores, regulae vestigiis suis parallelae moveantur sive eosdem ad rectas ad quas moventur angulos servent. Quod eminentiis quibusdam oblongis rectilineis, crenae cuidam eique in qua moventur, rectae congruentibus quas i n c r e n a t u r a s , nova sed necessaria voce appellare possis praestari constat.
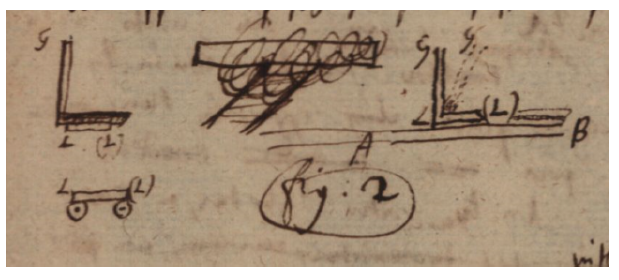
Qualis increnatura [Fig. 2] est L(L) qua regula GL movetur super AB in crena (L)B, eodem semper angulo GLA, sive is rectus sive obliquus sit, servato. Quod si increnatura velut rotulis quibusdam circa sua centra mobilibus imposita intelligatur, ne crenam in omnibus sui[s] punctis tangat; facilior erit motus.
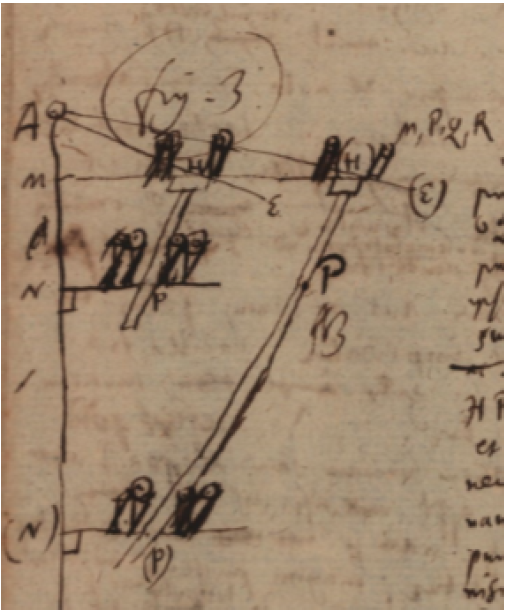
Ut autem aliquod motus in caetera omnia propagati principium intelligamus, cogitetur regula AE, mobilis circa B, in eodem semper plano ABE. quae elevata a situ inclinato ad minus inclinatum sive horizontali propriorem, aperiet Machinam, contrario vero motu, claudet. Quod ita intelligendum est[:] Dum AE elevabitur puncta G, H, I, K, quibus LG, MH, NI, OK, secat, longius distabunt sive recedent, ab L, M, N, O. Intelligantur jam regulae transversales GM, HP, IQ, KR, intersectionis puncta sequi, et rectae AE motu per parallelas LG, MH, NI, OK, eodem semper angulo dextrorsum duci, aut etiam dum AE rursus deprimetur sinistrorsum reduci: Eodem modo, motu transversalium GM, HP, IQ, KR, per parallelas, sustinentes G, H, I, K, mutabuntur M, P, Q, R puncta intersectionum cum aliis parallelis uno gradu semper inferioribus, MH, NPI, OQK, BRE. Pone jam effici, ut idem sit semper punctum intersectionis M, P, Q, R in parallela, MH, NPI, OQK, BRE, aliud vero atque aliud transversalis, GM, HP, IQ, KR punctum ei respondeat ( : quod ut mox dicam, facile effici potest : ) necesse erit ipsas MH etc. mutatione punctorum intersectionis M etc. in transversalibus GM etc. sursum deorsumque secundum longitudinem ipsius AB duci ac reduci quod facile intelligi potest ex fig. 3.
Pone enim in MH, ipsam HP; vestigiis suis parallelam incedere dextrorsum ope i n c r e n a t u r a e H. et NP ipsi MH parallelam esse. Manente puncto fixo P. in recta NP necesse est ipsam NP descendere ad (N)(P). Nam si mansisset ubi erat, a recta HP in (H)(P) promota in puncto P non amplius secaretur. Ut autem recta HP rectam NP non nisi in P. secare possit, duobus obicibus ex NP ipsa NP, perpendiculariter ad planum NMH exeuntibus effici potest, inter quos ipsa HP inclusa libere ludit, prorsus ut in exiguis naviculis remi inter duos obices manu agitantur, ita utcunque recta HP inter hos duos obices sursum deorsumque agatur nunquam tamen a puncto P inter eos intercepto dimovebitur. Eodem modo efficitur ut recta AE translata in A(E) punctum H et cum eo recta HP transferatur in (H) vel (H)P. Neque vero aliud quicquam hoc loco postulavimus. Ut autem motus eo facilior pariter et exactior sit; regulae ipsae inter obices interceptae aciebus suis alterutrum motui scilicet obstantem perpetuo prement; obex autem quilibet annulo sive tubulo sive si placet cylindro circa axem in quo fixus est obex, mobili, indutus erit ut fricanti regulae facilius cedat. Altrerutrum autem, aciem vel ex cylindrum ex chalybe durato esse fabricatum rationis est, altero ex aere fuso; quo minus motuum reciprocationibus alterantur. Apparet quoque, ut ad f i g. 1. redeamus, ab obice utrobique regulam motricem includente effici, ut quaemadmodum elevatione ipsius AE aperitur machina, ita ejus depressione rursus claudatur.
Quod si quis veretur, ne vacillationibus regulae motricis intra obices punctum intersectionis velut H, aut P, instabile reddatur; is consideret quantacunque sit latitudo vel libertas regulae intra obices ludentis; punctum tamen intersectionis tantum censeri, verbi gratia quo acies regulae cylindrum obici circumdatum aut ut mox dicam annulum
quendam obicibus interjectum tangit; quod semper durante motu, eodem in loco, aut aequipollente evenit. Fateor punctum contactus habere latitudinem quandam, et repetitis contactibus; una scilicet regula aliam ducente, latius errorem propagari; sed fieri tamen arte potest, ut posterior error priorem non augeat, sed quodammodo compenset; certa semper lege, quamdiu acies aut cylindros non diminutos ponimus: cum etiam ipsa diminutio temporis tractu facta quae tamen ita subito non sentietur. Supra remedium non sit. At inquies punctum contactus non esse idem in reducendo quod in ducendo, quia oppositus tunc obex premitur: sed hoc nihil turbat; quia in qua operatione ductuum ratio habetur, in ea reductuum non habetur. Effici tamen etiam potest, idque malim, ut regula obicibus intercepta sit instar prismatis Triangularis trium acierum, quarum duobus obices oppositos; una annulum quendam in P nonnihil incisum et circa centrum suum in rectave axem NI mobilem tangat, ita punctum P, semper erit idem tam in ducendo quam in reducendo praesertim cum ipsa HP, durante operatione eundem semper faciat angulum ad ipsam NI, adeoque ad incisuram in qua est annulus P, quod si pro alia operatione mutetur angulus HPN. Nihil prohibet cochlea exigua etiam annuli P inclinationem mutari, ut scilicet ad axem annuli, angulus rectae HP semper sit rectus. Idem in
obicibus quoque locum habet ut in eosdem semper circellos cylindris eorum incisos acies intrent. Facile autem cavebitur ut mutatio inclinationis clausa tantum machina fieri possit, durante motu non possit. Clausa autem machina sponte sua nulla peculiari manuum opera mutatam ipsius HP inclinationem consequetur laxato tunc retinaculo quodam, quod alias durante prius motu obstabat inclinationis mutationi.
Praeterea ut increnaturarum aut acierum, quibus in crenis aut incisuris moventur regulae, impediatur vacillatio; faciendum est, ut eadem acies diversis incisuris sic satis invicem remotis, at perfecte parallelis et similibus, recipiatur. Nec refert quod ad exactitudinem summam omnia necesse est constructa esse, unde difficilis erit motus, nam cum celeritas non postuletur; magna profecto impedimenta necesse est quae vectis longitudine et si velis agentis vectem cochleae tarditate non vincantur. Cumque necesse sit aliquando puncta quaedam diversarum regularum, dum praeparetur machina ad novam operationem, in eadem esse recta imaginari, hoc exacte praestari poterit quodam dioptrae genere si perforata in punctis quaesitis utraque regula, lux per omnia puncta radiet; aut videri possit. In elaborandis autem machinae partibus perspicilia adhibere artificem rationis erit; cum sit instrumentum hoc summae exactitudinis specimen futurum.
Innumera alia ab industrio artifice pro re nata excogitabuntur ut appareat quousque humana diligentia in elaborando tantae utilitatis instrumentum proficere liceat. Quo omnes algebrae aequationes resolvuntur, et Geometriae rectilineae, ejus certe quam Vieta et Cartesius ad analysin reduxere, problemata solvuntur; et curvarum omnium a Cartesio in classes distributarum fructus hactenus contemplationem non egressus continetur. Sed haec postea exponam. Nunc absolvenda Machinae constructio est motusque, neque enim constructio sine motu commode explicari potest. Nimirum r e d e u n d o a d f i g. 1 elevato primo mobili AE motu circa centrum A regula transversalis GM, procedit in ipsa LG directione seu dextrorsum, quod fieri non potest, quin parallela (horizonti) MH moveatur in recta ANB directioni NB seu deorsum. Interea temporis transversalis HP, ob eandem ipsius AE elevationem movetur in MH sinistrorsum; quare NPI cui HP occurrit in P, et ibi inter duos obices modo explicato intercipitur descendet. Eodem modo eodem tempore; transversales, IQ, KR, et si quae aliae sequuntur movebuntur sinistrorsum, parallelae OQK, BRE etc. deorsum, quod ludi genus continuabitur, quousque postulabit necessitas, et salva exactitudine sufficient vires.
Hactenus hujus plani nempe ABE explicatae partes, explicandae nunc et alterius DCF, ipsi paralleli et similiter positi, partes an plerisque similes. Praeter ea scilicet quae admonebo. Nimirum DS regula immobilis sit ipsi CF, vel BE parallela, et puncta A. D. S: sint in eadem recta. Efficiatur autem arte quadam, ut dum punctum G procedit sinistrorsum vel recedit dextrorsum, ob motum elevationis et depressionis ipsius AE circa centrum A; punctum S, mobile procedat in recta DS in eundem sensum, directione scilicet DS, dextrorsum, ( : etsi in pagina sive figura id sit sinistrorsum quoniam utraque plana ABE, DCF, non in eodem plano jacentia, ut illic repraesentantur, sed parallele erecta censenda sunt : ) vel recedat, directione SD, sinistrorsum; ea tantum lege, ut DS. sit semper media proportione inter AL, et LG. et regula quaedam SF, cum puncto S procedens, et tamen circa centrum S: mobilis, sit semper ipsi AE parallela. Quae duo qua ratione obtineri possunt postea explicabo. Nunc eo supposito intelligatur transversalis ST, cum puncto S procedens propellere sursum deorsumque in recta DC. parallelam (horizonti) TV ; et motu ipsius SF in ipsa TV , aliam duci transversalem V X a qua rursus parallela (Y )Z in ipsa DC. sursum deorsumque ducatur. Idem intellige de transversalibus
Zα, βγ, δθ quae in parallelis (Y )Z, λβ, μδ, ab ipsius SC motu huc illuc ducuntur, eodem angulo servato; et parallelas (unaquaeque ei in qua ducitur inferiorem,) λαβ, μγδ, CθF in recta DC. sursum deorsumque agunt. Puncta autem T. X. α. γ. θ. sunt in perpendicularium DTC, SX, Vα, Zγ, βθ (quae omnes ex apta prima imaginariae sunt, et parallelarum, quae omnes reales rigidaeque sunt VT, ZX(Y), βαλ, δγμ, FθC, intersectionibus.
Superest ut explicetur transitus de plano in planum, seu modus quo efficitur, ut DS sit media proportionalis inter AL et LG. et ut SF perpetuo maneat parallela ipsi AE. Porro recta AL durante motu manet situ et magnitudine eadem, at LG perpetuo mutatur magnitudine, manet situ; idemque erit de recta DS, caeterae situm pariter et magnitudinem mutant. Jam parallelismum ipsarum AE, SF perpetuum, ita obtinebimus; ponatur Y in recta AY ipsi BE parallela punctum Y ita procedere ut recta AY semper aequetur ipsi DS, seu ut sit media proportione inter AL et LG. quod modo postea explicando, obtinebimus. Eo autem supposito intelligatur alicubi in recta AE, punctum quoddam fixum ξ, unde dextrorsum prodeat recta indefinita, parallela ipsi BE inque ea sumatur ξπ aequalis ipsi AY jungantur puncta Y et π regula solida Yπ. Patet manente AY , utcunque elevetur aut inclinetur AE, latera opposita rhomboeidis AξπY. manere parallela; quaemadmodum instrumenti qui vulgo ad parallelas ducendas utuntur, quod ab officio rectissime parallelogrammum appelles. Hic vero illud praeterea addendum est ut latus Yπ in rectis indefinitis AY, ξπ huc illuc incedere possit. Ex punctis Y, et π, exibunt duae lineae rigidae, YS, πσ duo plana ABE, DCF perpendiculariter jungentes,
et regulam Yπ regulae Sσ connectentes, unde Sσ vel SF, ipsi Yπ, vel AE perpetuo parallela incedet erit, quod faciendum erat.
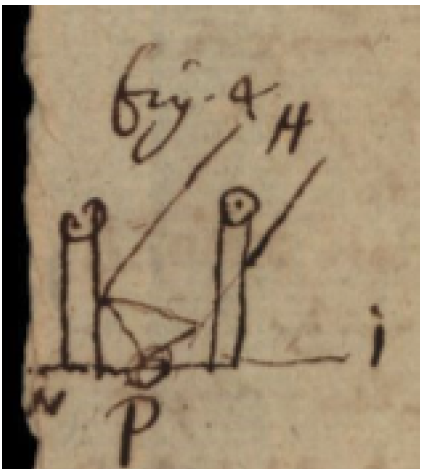
Ut autem recta AY semper media sit proportionalis inter rectam constantem AL et continue variatam LG paulo difficilius est: quod tamen ni fallor ita consequemur; inspiciatur fig. 1 aut, quae sane ejus partem clarius explicat, figura 5.
Punctum G. motu elevationis aut depressionis rectae AE vel Aξ circa A ducat secum perpendicularem Gφ. qvae rursus in recta AYφ ducat ipsam φψ, angulo ψφA constante semirecto, quae rectam LAψ secabit in ψ. Ergo Aψ aequabitur ipsi Aφ vel LG. Recta φψ in eodem puncto ψ, secet aliam rectam Yψ quae recta in radio LY huc illuc moveri possit, servato angulo, constante recto ψYL. Radius autem LY mobilis esto circa centrum L, Ponendo jam rectam φψ duobus obicibus in ipsa Yψ plantatis inclusam esse, ut punctum intersectionis ψ in recta Yψ semper constans esse possit; sequetur rectam Yψ ab ipsa φψ duci. Quod si ergo radius LY circa centrum Y mobilis non esset, moveretur ipsa Yψ secundum longitudinem ipsius LY , ob motum ipsius φψ, sed quoniam desideramus praeterea ut punctum Y semper maneat in eadem recta Aφ; quod fibula quadam ipsi Yψ infixa et in rimam ipsius Aφ intrante, inque ea huc illuc mobili efficietur: ideo ut Triangulum rectangulum ψYL omnes formas induere possit, necesse erit LY mobilem esse cica L. Erit ergo AY semper media proportionalis inter AL et Aψ seu inter AL et LG utcunque varietur punctum G. Quod faciendum erat. Unde jam antedicta consequuntur.
Explicata est constructio Instrumenti Algebraici, ut appareret, ex quibus partibus compositum sit, et qua ratione partium motus alter alterum regat. Nunc superest, ut modum quoque tradamus utendi Instrumento ad Aequationum radices Geometrice, in lineis, et quod hinc sequitur Mechanice in numeris quantumlibet vero propinquis, inveniendas. Constat ex iis quae Vieta inprimis et Cartesius, tradidere, omne Problema (ordinarium, rectilineum) determinatum, reduci posse ad aequationem in qua una tantum incognita supersit; secundum quam ordinata aequatio eo usque assurgere censebitur quo usque maxima incognitae dimensio excrevit. Praeterea tradita est a Cartesio methodus efficiendi, ut omnia aequationis loca sint repleta, et ut omnes aequationis radices sint verae, ut ille loquitur, id est affirmativae: quo facto, magno commodo nostro, feliciter evenit ut signa + et – in aequatione sese alternis sequantur, quod quam sit instituto nostro necessarium mox apparebit. Sumamus in exemplum aequationem ex decem terminis compositam, sive noni gradus, ( : raro enim altius assurgetur : ) quae ad radices affirmativas praeparata, atque ordinata, ita stabit:
y^9-by^8+acy^7-a^2dy^6+a^3ey^5-a^4fy^4+a^5gy^3-a^6hy^2+a^7ly-a^8m=0et transponendo, ut signa negativa amoveantur:
☉ a^8m+a^6hy^2+a^4fy^4+a^2dy^6+by^8=a^7ly+a^5gy^3+a^3ey^5+acy^7+y^9
Ubi patet duas haberi summas sive formulas aequales inter se, alteram omnium terminorum exponentium parium, 0. 2. 4. 6. 8. alteram imparium, 1. 3. 5. 7. 9. Nec vero necesse est terminum summum, hoc loco y^9 purum esse, nullaque quantitate cognita affectum: cum contra in nostro sit arbitrio purum reddere quemlibet, posito enim a esse unitatem, et omnia dividi per m, fiet aequatio:
☽ 1+hmy^2+\displaystyle\frac{f}{m}y^4+\frac{d}{m}y^6+\frac{b}{m}y^8=\frac{l}{m}y+\frac{g}{m}y^3+\frac{e}{m}y^5+\frac{c}{m}y^7+\frac{1}{m}y^9
Illud quoque constat pro Unitate assumi posse quamlibet quantitatem datam, prout commoditas operationis exigere videbitur.
His ita positis, ajo aequationem ☽ in machina ita perfecte repraesentari, ut satis appareat ipsam rerum naturam, ad hoc construendi genus invitare, subsidiis dudum velut consulto praeparatis, ut facilius exitum reperiret. Nam durante motu, quomodocumque linearum magnitudo varietur, attamen AL appellata 1, et DS appellata y, sive LG, y^2 semper verum erit ab uno latere esse
\displaystyle AL=1 \ LM=\frac{h}{m}y^2 \ MN=\frac{f}{m}y^4 \ NO=\frac{d}{m}y^6 \ OB=\frac{b}{m}y^8\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \Bigg\{ ab altero latere vero
\displaystyle DT=\frac{l}{m}y \ T(Y)=\frac{g}{m}y^3 \ Yλ=\frac{e}{m}y^5 \ λμ=\frac{c}{m}y^7 \ λC=\frac{1}{m}y^9Quod si ergo durante motu aliquando evenit, ut DT+T(Y)+(Y)λ+λμ+μC, id est DC, fiat aequalis ipsi AL+LM+MN+NO+OB, id est AB, sive ut punctum C plani unius e regione respondeat puncto B plani alterius, id est ut recta imaginaria BC sit utrique plano perpendicularis, quod in media operatione, etiam machina non detecta, ope styli cujusdam impingentis, facile sentiri potest; tunc manifestum est, etiam \displaystyle 1+\frac{h}{m}y^2+\frac{f}{m}y^4+\frac{d}{m}y^6+\frac{b}{m}y^8 aequari ipsi \displaystyle \frac{l}{m}y+\frac{g}{m}y^3+\frac{e}{m}y^5+\frac{c}{m}y^7+\frac{1}{m}y^9 ac proinde si machina in eo statu sistatur, quae tunc fuerit DS sive y, eam fore quaesitam, cum aequationi propositae satisfaciat. Quod si Aequatio ☉ commodior videatur ad usum quam aequatio ☽, ne scilicet omnia per m dividere necesse sit; aut etiam si alium quemlibet terminum potius quam ultimum purum reddere velimus, id factu facillimum erit, si modo tunc postuletur, ut punctum C respondeat ex adverso non ipsi puncto B, sed puncto ω, sumta recta Bω tali, ut sit differentia inter terminum cognitum sive ultimum, et unitatem; sumta inquam recta Bω a B versus A, cum unitas est maior termino ultimo, aut in contrarias partes, producta AB ultra B, cum est minor. Quod, si ad aequationem ☉ applicetur, posito a esse unitatem, sive 1, erit terminus ultimus sive cognitus, m. cumque necesse sit AL + vel — Bω aequari termino cognito m, ut scilicet caeteris rectis LM,
MN etc. reliquos terminos repraesentantibus, tota aequationis ☉ portio sinisterior, sive exponentium parium, a recta Aω repraesentetur; ideo + vel — exprimendo per signum ambiguum \pm, habebimus, 1 \pm Bω=m sive \pm Bω=m-1, vel Bω= \pm m \mp 1 id est Bω erit
differentia inter m et 1. et quando m maior quam 1. tunc pro Bω= \pm m \mp 1: scribemus Bω=m-1. Eritque m=1+Bω adeoque Bω non subtrahetur ipsi AB, seu addetur, sive sumetur in recta AB producta ultra B. Contra quando 1 major quam m, tunc pro Bω= \pm m \mp 1, scribetur Bω=1-m, adeoque erit m=1-Bω . Quod significat Bω, a recta AB subtrahendam, sive in contrarias partes sumendam esse regrediendo a B versus A.
Itaque regula mobilis parallela BE, ascendendo descendendove secum aget affixam sibi, et in ipsa AB mobilem regulam Bω et ex ejus puncto ω exiens perpendiculariter stylus impinget in puncto C regulae mobilis FC, tunc cum rectae Aω, et DC, fiant aequales, seu cum DS est quaesita. Cumque manifestum sit quamlibet cognitam sumi posse pro unitate sive AL, et terminum quoque cognitum sive ultimum aequationis cujusdam valorem quemlibet pro arbitrio nostro accipere posse; sub literis quoque a, b, c, d, e, f, g, h, l, m, intelligi posse quantitates cognitas quaslibet; et in aequatione qualibet effici posse, ut quantitas cognita alicujus termini sit data, ideo imposterum formula ☉ uti suffecerit cum
caeteras omnes comprehendat.
Explicandum ergo nunc est, qua ratione Instrumentum aequationi cuilibet propositae accommodetur, sive qua re quomodo effici possit, ut sit:
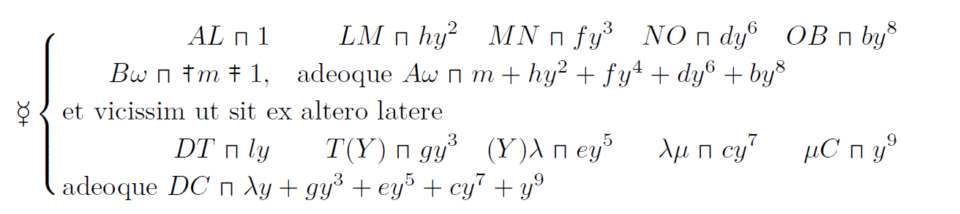
Ut scilicet in casu aequalitatis rectarum Aω, DC incognita y haberi possit. Hoc autem ita praestabitur, in fig. 1. regula LG moveatur, sursum deorsumve in recta AB, donec fiat AL aequalis ipsi a: seu unitati assumtae. Quo facto et radius AGE, tamdiu moveatur circa centrum A, donec rectam LG ita secet in puncto G, ut fiat LG aequalis ipsi AL, sive unitati. Jam regula transversalis GM, circa punctum G, in CM regulae increnatura qua per ipsam LG incedit fixum eousque moveatur, donec ipsi LMB occurrat in puncto M tali, ut ipsa LM valeat h. Quo obtento in eo situ sive inclinationis angulo LGM, ita firmabitur regula transversalis GM, ut durante motu sive operatione exempli prasentis inde dimoveri non possit. Idemque de caeteris transversalibus intelligendum est, earum inclinationem manuum opera mutari pro lubitu posse, quando Machina operationi praeparatur; durante operatione mutari non posse, quod effectu facillimum esse, nemo dubitat. Itaque angulus LGM, vel distantia regularum LG, MH, sumatur talis, ut sit LM=h. Eodem modo angulus MHP vel NIQ, vel OKR talis ut distantia MN sit f, NO sit d, OB sit b. Quid simplicius? Similiter anguli DST, TVX, (Y)Zα, λβγ, ηδθ, tales sumantur ut sint distantiae DT=l, T(Y)=g, (Y)λ =e, λμ=c et μC=AL=1.
Quo facto Instrumentum erit praeparatum, et ajo perpetuo eventurum, durante machinae motu, utcunque elevetur aut deprimatur radius AE, circa centrum A, ut manente AL=1 et DS continue variante appellata y, locum habeant aequationes sive valores rectarum LM, MN, etc. item DT, TY , etc. recensiti sub signo ☿.
Quod ita demonstro, etsi Geometrae intelligenti rem sine demonstratione ex dictis manifestam putem. Ex punctis G, H, I, item s. v. z. β in rectas MאH, NPבI, OQגK, BRE item TדV, (Y)XהZ, λαלβ, μγשδ, CθF demittantur perpendiculares imaginariae GאP, HבQ, IגR, SדX, Vהα Zלγ, βשθ. Jam vero cum sit AL=1, DS=y, erit LG=y^2, quia LG inter AL et DS proportione media est, ex constructione. Hinc sequitur LM esse hy^2 quoniam initio motus cum LG esset unitas = AL, puncto G in (G) existente, et puncto M in (M) erat L(M)=h. Patet ergo angulum GLM, aequalem semper angulo (G)L(M) esse talem, ut LM sit aequalis producto ex multiplicatione ipsius LG per f. Nam LM est ad L(M) seu ad h ut LG ad L(G) seu ad 1. Ergo LM=\frac{LG \ multiplicata \ per \ h}{divisa \ per \ 1}. Et quia LG=y^2, ex dictis, erit LM=hy^2.
Eadem methodo et caetera demonstrantur, nam quia LM vel Gא est hy^2, ideo אH erit hy^4, cum in quolibet Triangulo ipsi ALG simili, quale est GאH, altitudo ut Gא per y^2 multiplicata det basin ut אH. quandoquidem אH est ad Gא, ut y^2 ad 1. seu ut LG ad AL. Adeoque אH=\frac{Gאy^2}{1} sive hy^4. Porro cum y^2 esset 1. seu LG=AL tunc אH erat h. eodem autem tempore per praeparationem instrumenti paulo ante factam MN, sive אP erat f. Idem autem semper manet angulus אHP, etiam in progressu operationis, ergo ut אP erat ad אH tunc cum y vel y^2, esset 1, seu ut h ad f, ita nunc quoque quocunque assignabili motus momento, qualiscunque sit y^2 vel LG; אP ad hy^4, sive אH erit; nempe \frac{אP}{hy^4}=\frac{f} {h}. ergo אP=fy^4=MN. Iisdem prope verbis ostendetur NO, vel בQ semper valere dy^6 et OB, by^8. In altero plano, patet DT esse ly, nam tunc, cum DS vel y esset 1. DT erat l, ergo tunc erat DT ad DS, ut l ad 1. At eadem perpetuo manet ratio ob eundem semper angulum DST, ergo nunc quoque cum DT valet y. DS vel Sד valebit ly. Hinc porro sequitur, דV valere ly^3 quoniam SF, parallela ipsi AB, unde Triangulum SדV simile Triangulo ALG, adeoque דV ad ly seu Sד, seu ut AL ad LG seu y^2 ad 1. Unde T(Y) vel דX=gy^3. Nam quando y est unitas דV sive ly^3, erit l, jam ex praeparatione, quando y est 1, דX aut T(Y) est g. Est ergo tunc דX ad דV ut l ad g. Jam eadem semper manet ratio, quoniam idem durante motu angulus דVX. et proinde Triangulum VדX semper simile manet; quare semper דX ad ly^3 sive ad דV ut g ad l, sive \frac{דX}{ly^3}=\frac{g}{l}, unde דX=gy^3=TY. Iisdem prope verbis ostendetur Yλ sive הa valere ey^5, et λμ, cy^7, et μc, y^9. Ac proinde veritas aequationum omnium sub signo ☿ recensitarum ostensa est.
Quoniam vero eadem aequatio plures habere potest radices reales, hinc etiam toties durante machinae motus evenire debet, ut Aω et BC, fiant aequales, ac proinde una eademque operatione invenientur radices Aequationis omnes, quod in numerosa potestatum resolutione qualem Vieta invenit, non procedit; hoc loco autem in numeris non minus quam lineis praestatur. At, inquies, ignorari quousque motus continuari debeat, ad radices omnes inveniendas. Respondeo per doctrinam de Aequationum determinationibus sive limitibus facile praefiniri terminos, quos y inutiliter excedat: Sed et sine calculo, manifestum est, cum hoc loco omnes radices sint verae, maximam ex ipsis, esse termine cognito secundo, summae scilicet omnium, minorem. Quare inventis etiam aliquot ex ipsis, facile et summa residuarum, quam maxima ex ipsis excedere non possit, cognoscitur. Quantitatem autem qualibet aequationis propositae radice minorem haberi necesse est, non enim perinde decrescendo, ut crescendo in infinitum iri potest; facile enim ad finem motus regrediendo sive claudendo machinam pervenietur; ut proinde radicem si qua est inferior unitate, occurrere necesse sit. Porro inventae in lineis radices, facile in numeris habentur, quamtumlibet exactis, si circino ad scalam quandam quantum satis est subdivisam transferantur. Unum desiderari dicet aliquis, ut scilicet radices in numeris veris
habeantur, quando sunt rationales, quod praestat calculus Vietae. Sed quanquam ad usum, id necesse non sit, ausim tamen ab hac quoque machina promittere. Nam statim agnoscetur, si divisores ultimi termini, inventis radicibus proximi, aequationem multiplicatione producere potuerunt. Idem etiam re ad numeros non reducta ( : constructio
enim per instrumenti naturam pure Geometrica est : ) ad radices aequationum literalium rationales, si quae sunt, facile agnoscendas sufficit. Breviter ab hoc instrumento unico tantum momento praestatur in lineis quantum in Geometriam a Cartesio introductis; et in numeris quantum calculo praeclare sane sed mire anxio et impedito, a Francisco Vieta
invento: ut nesciam an in eo genere aliquid ultra exactam Instrumenti elaborationem vel optari possit. F i n i s.