See a transcription for the manuscript
Translation of Periodus numerorum (1705?)
0_{512}1_{512}|0_{256}1_{256}|0_{128}1_{128}|0_{64}1_{64}|0_{32}1_{32}|0_{16}1_{16}|0_{8}1_{8}|0_{4}1_{4}|0_{2}1_{2}|0_{1}1_{1}=N
19\ \ \ \ \ \ \ \ \ \ 18\ \ \ \ \ \ \ \ \ 17\ \ \ \ \ \ \ \ \ 16\ \ \ \ \ \ \ 15\ \ \ \ \ \ \ 14\ \ \ \ \ \ 13\ \ \ \ \ 12\ \ \ \ 11\ \ \ 10
= Period of Natural Numbers in Dyadic Columns.
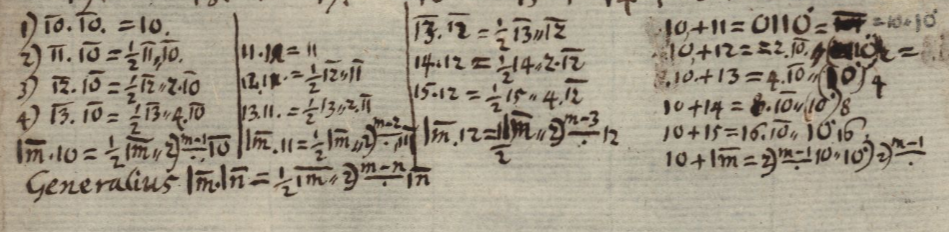
0_{1024}1_{1024}|0_{512}1_{512}|0_{256}1_{256}|0_{128}1_{128}|0_{64}1_{64}|0_{32}1_{32}|0_{16}1_{16}|0_{8}1_{8}|0_{4}1_{4}|0_{2}1_{2}|0_{1}1_{1}=0
20\ \ \ \ \ \ \ 19\ \ \ \ \ \ \ \ \ \ 18\ \ \ \ \ \ \ \ \ 17\ \ \ \ \ \ \ \ \ 16\ \ \ \ \ \ \ \ 15\ \ \ \ \ \ \ \ 14\ \ \ \ \ \ 13\ \ \ \ \ 12\ \ \ \ 11\ \ \ 10
=0= Period of Natural Numbers written in a Dyadic form in single Columns.

Calculation RULES
1. In this case, the single characters are not multiplied
by every co-multiplier, as in other cases,
But rather the single characters [are multiplied] by the single corresponding ones
In this case in fact, it is not computed sideways and Number by Number
but descending Period by Period
2. If a corresponding Period doesn’t fill the whole place of the
next one, it shall be repeated as many times until it fills it.
For, once the same period is repeated, a Period of the
Same Column still remains
3. Multiplying by 0 returns 0 itself, 1 returns the co-multiplier
Adding 0 returns the co-addend, 1 returns the anti-co-addend
so that is equal to 0˙ with a carry
0˙, by adding a carry of 1, gives 1 with a carry and by adding 1 to this one gives 0˙˙ etc.
4. Every carry adds a Unit [RK1] to the higher nearest Column
A double carry adds a unit to the higher column shifted by one place
A triple carry adds a unit in the same place and so
A unit to the analogous next place of the higher column
A quadruple carry adds a Unit to the higher Column shifted by two places etc.
